
Reconstructing Shakespeare's second Globe using 'Computer Aided Design' (CAD) tools

Reconstructing Shakespeare's second Globe using 'Computer
Aided Design' (CAD) tools
Tim Fitzpatrick
Department of Performance Studies, University of Sydney
tim.fitzpatrick@arts.usyd.edu.au
Fitzpatrick, Tim. "Reconstructing Shakespeare's Second Globe using 'Computer
Aided Design' (CAD) tools." Early Modern Literary Studies Special
Issue 13 (April, 2004): 4.1-35 <URL: http://purl.oclc.org/emls/si-13/fitzpatrick>.
This article describes a research project which used computer-aided design
(CAD) in an attempt to understand the structural features implicit in Wenzel
Hollar's 1630s sketch of the second Globe playhouse in London. It focuses
on assumptions about and interpretations of the sketch implicit in such
an enterprise, and on the advantages and limitations of using CAD in this
way. The importance of the second Globe in attempts to arrive at an understanding
of the structure and size of the first Globe, Shakespeare's original playhouse
is due to the generally held belief that the second was built on the foundations
of the first (destroyed by fire in 1613). The Czech panoramist Wenzel Hollar
made a sketch of Southwark in the 1630s from atop the tower of Southwark
Cathedral, and it shows in the middle distance the second Globe shortly
before the playhouse was razed by the Puritans:

(Figure 1. Hollar's view of London, looking west (Yale Center for British
Art, Paul Mellon Collection))
John Orrell's interpretation of Hollar's work as the product of minutely
accurate topographic draughtsmanship (1983: chapter 4) has been one
of the major factors which have led to the third Globe's being 100' in diameter.
However in an article in Shakespeare Bulletin (1996) I argued that
the second Globe playhouse which appears in Hollar's drawing might have
been a smaller 16-sided ad quadratum building 86' in diameter. I
outlined there the mathematical basis for such a proposal, argued that such
a configuration would fit the archaeological remains, and suggested that
Hollar's drawing is a partly inked-over pencil sketch, of no real use for
calculations such as those done by Orrell. As will be demonstrated below,
I believe that my dismissal of the topographic accuracy of Hollar's sketch
is not the end of the matter, and that even as a sketch it might still reflect
accurately some possible structural configurations of the building Hollar
saw, thus offering invaluable information—if not about the dimensions of
the building, at least about the geometrical and architectural relationships
between its components. This article therefore describes an analytical strategy
involving CAD in an attempt to account for significant features of the sketch
and to subject it to analysis. I suggest that it is possible that the object
which Hollar was sketching was a 16-sided ad quadratum polygon with
two stair turrets equidistant from its main axis of symmetry, and a stage
cover structurally integrated with the polygon; that such a theoretical
object is consistent with the archaeological remains; and that Hollar's
sketch may be an accurate rendering of such a building.
Interpreting the Hollar sketch
Serious attention to Hollar's sketch began in the 1970s. Paradoxically,
it has suffered multiple 'corrections' for supposed inaccuracies of detail,
yet has been used as the basis for complex trigonometrical calculations
as part of an attempt to establish the size of the original Globe. Substantial
work on the sketch and subsequent engraving was done by C. Walter Hodges
(1973) in Shakespeare's Second Globe: The Missing Monument, and by
Richard Hosley (1981), both of whom suggested that Hollar's work was an
inaccurate representation of the playhouse, particularly in regard to the
positioning of the external stair turrets. However if the archaeological
evidence (discussed in some detail below) is to be taken seriously, features
of their work must now be questioned; I have discussed this in detail elsewhere
(Fitzpatrick, 1999).
The most radical interpretation of Hollar was that propounded by John Orrell
in his 1983 book, The Quest for Shakespeare's Globe. He took over
without question Hodges' projection (1983: 123) which would rotate the right-hand
stair turret to make its façade invisible, but did not go into a detailed
consideration of the polygonal configuration of the building as Hosley had
done. Instead he continued a line of research concerned with the size of
the building which Hollar has sketched. In 1981 Hosley (82) suggested the
Globe must have been around 100' across, given that the height of the polygon
to the eave-line is around 1/3 of the width of the building—and as the Fortune
was 33' to the eave-line (and we might expect a similar height at the Globe)
the Globe would have had a diameter of around 100'. Such thumbnail calculations
(and the adjective is used advisedly, since that is roughly the size of
the building in Hollar's original sketch) were both superseded and validated
by the complex trigonometrical calculations done by Orrell for his 1983
publication. And herein lies his re-interpretation, a complete conceptual
re-evaluation of the work: he argued that Hollar's sketch is an extremely
accurate topographic drawing and, since this playhouse was most probably
built on the charred foundations of the first, that conclusions as to its
layout should also be relevant to the size and configuration of the first
Globe (103, 121).
However, as evidenced in a previous article (1996: 8-10), my first examination
of the original drawing at the Yale Center for British Art in 1995 convinced
me that Hollar's is not the topographic drawing Orrell believed it to be,
but is rather a freehand sketch based at most on limited topographic sightings,
disqualifying it as a basis for the sorts of complex and precise trigonometrical
calculations from which Orrell arrived at a second Globe (and hence at a
first and a third Globe) around 100' in diameter. Orrell has conspicuously
avoided responding to these arguments in his response to that article, choosing
merely to reassert his opinion that Hollar's is a "painstaking drawing"
(1998: 5).
I have now examined the sketch on three separate occasions, and subsequent
examinations have only confirmed my original claim that this is indeed a
sketch. A more detailed discussion of the implications of my most recent
research is the subject of a forthcoming article, but in the present context
it is relevant to present a brief summary of the issues. Orrell's claim
that this is the carefully-drafted result of a multitude of sightings through
a topographic glass ("a table of indexical signs, each line caused
by a line in reality, each proportion answering to the proportions of the
real scene." [1983: 75]) is simply unsustainable. A number of art historians
with whom I have discussed the work agree that it simply looks like a sketch.
In the most distant parts of the panorama the sketching is 'sketchy' indeed,
buildings delineated with a few broad strokes. In the middle distance, where
the Globe is located, the sketching is detailed and at times almost obsessively
so; but it is clearly sketching, with the sorts of multiple passes evidenced
above. There may be some topographic sighting, but tell-tale marks (such
as I have suggested might be evidenced in the 'finial' markings on the Globe)
are few and far between.
Further impugning Orrell's interpretation are doubts about how the image
which he claims was viewed and recorded through the topographic glass was
transferred to the drawing paper. In The Quest for Shakespeare's Globe,
he suggested that with drawing frames transfer was accomplished by correspondence
between grid-lines on the frame and grid-lines on the drawing paper, but
that with the glass another technique was used: sightings through the glass
were marked directly on the glass itself, and then traced onto the paper
by simply holding the paper, clipped to the glass frame, up to the light
(1983: 22, 26; 1993: 7). Unfortunately neither the frame nor the glass techniques
which Orrell outlines can have worked for the Yale object. Firstly, it shows
no signs at all of having been gridded up to match grid-lines on a drawing
frame. More importantly, it is extremely thick paper, and no amount of holding
it up to the light will allow a traceable image on the glass to show through.
Any such tracing would therefore have to have been done first onto fine
tracing paper, and this traced image would then normally have been transferred
to the heavier drawing paper by the common practice of 'pin-pricking' referred
to by Martin Kemp (1990: 170, 176). The disadvantage of such an alternative
process is that it involves two possible sites for transmission errors,
rendering the final image less than authoritative—but, more significantly,
such a process is not supported by the Yale original: there is no evidence
of pin-pricks on Hollar's drawing paper.
It is doubtful that any of the three scholarly interpretations discussed
so far has been based on sighting Hollar's original at Yale, since some
of the pronouncements made by their proponents are clearly the result of
working from photographic reproductions. My previous article questioned
John Orrell's characterisation of a number of creases in the paper as pencil
lines (1996: 10). In Quest Orrell admits to not having seen the original,
calling instead on the authority of Richard Hosley (1983: 101); Hosley might
have seen the sketch at some point, but certainly not before his 1981 article
where he suggests that some of the markings are "Stigmata caused apparently
by a tear in the drawing" (1981: 90). In reality the marks he refers
to are a combination of pencil and ink lines and a paper crease (feature
L in Figure 3 below). C. Walter Hodges' interpretation of the relationship
between the original pencil markings and the pen markings (as reported in
Gurr et al, 1993: 12-13) does not indicate direct contact with the original
drawing, since he ignores pencil lines that are clearly there, and sees
independent pencil lines where there are none; this suggests he is working
from a possibly degraded copy.
While the authority of these scholars has given their pronouncements considerable
weight, the paradox embedded in the received wisdom must cause concern:
Hollar has given us an artifact of painstaking draughtsmanship, yet he errs
unaccountably in important details. The following discussion will suggest
that both parts of this proposition are problematical: I will argue that
it is not substantially a topographic drawing, but that even as a sketch
it offers invaluable evidence.
Wenzel Hollar's two pencil and pen sketches, made in preparation for his
renowned panorama of London, are now in the Paul Mellon collection at the
Yale Center for British Art. They were made in the 1630s from a vantage
point atop the tower of St Saviour's or Southwark Cathedral. One of them
looks west and includes the second Globe. Hollar first used pencil in a
process which I suggest shows characteristics of a sketch rather than a
topographic drawing, and then inked part of the pencil sketch, with the
ink markings not necessarily tracing accurately the pencil marks. He then
did a second substantial redrawing of this 'original' for his engraved panorama,
an operation which involved a change of point of view, with an anti-clockwise
shift of the central axis of the building.
An enlarged reproduction of the detail of the Globe from Hollar's sketch
and a schematic diagram labelling the symptoms of such a sketching process
are reproduced below as Figures 2 and 3. Various features of Hollar's sketch
are notated alphabetically in Figure 3, and will be referred to at various
points in the following discussion:

(Figure 2. A recent photographic enlargement of Hollar's drawing of the
Globe. (Yale Center for British Art, Paul Mellon Collection))

(Figure 3. A schematic diagram of the pertinent features of Hollar's drawing)
The main structure is portrayed as a circular drum, though for various
reasons we must assume that this is in fact an approximate representation
of a multi-sided polygonal structure. I assume that the curved lines representing
the roof ridges and eave-lines of the polygon (A, B, C, D) are 'inaccurate'
in the sense that they are curved approximations of a series of straight
lines that would make up the roof-sections of the bays of the polygon. We
can also note initially, in regard to calculations of size, that there is
some confusion at the left of the building: its multiple verticals (P) and
three short 'base-lines' (S) offer no automatic indications of a 'correct'
width and height of the building. Attached to the polygonal drum at various
points are three rectangular structures: two stair turrets on its outer
circumference, and a large stage cover attached at or near the outer circumference
at the left of the drawing, and perhaps attached to the inner circumference
at or near the mid-point of the yard. The angular relationships between
the three rectangular structures are definable within certain limits: the
stair turrets are separated by less than one-quarter of the circumference
of the drum; we are looking almost frontally at the nearer one, which is
close to the centre of the building as we see it, yet the facade of the
right-hand one is obliquely visible. As can be seen in Figure 3 above, the
angle (b) between the stair turrets seems in the range 60 degrees and 80
degrees. Second, the angle (a) between the nearer turret and the line of
the M-shaped double gable seems in the range 40-50 degrees, and the point
at which the stage cover connects to the outer circumference of the polygon
is about a quarter-way or 90 degrees around from the
nearer stair turret. Further, the central nick in the M-shaped double gable
is almost perfectly aligned with this nearer stair turret: if our point
of view has us looking through the side wall of the stair turret down a
radius of the drum, then the central nick of the stage cover (G) is also
very close to that radial, that is, very close to the centre of the building,
the mid-point of the yard.
This nearer stair turret is the most detailed part of sketch: the precision
of both the tiling shown on the left-hand side of its roof and the shadow
it is casting to its right on the polygon proper (E, F) suggests that it
cannot easily be discounted as an error or aberration as has been the tendency.
The exposure of the left-hand side of the roof indicates that this nearer
stair turret is rotated or angled away to the viewer's right, despite the
fact that it is at or very close to the centre of the sketched building
(and therefore would be pointing directly at us if it were following the
radial geometry of the drum). The remains excavated in 1989 established
that the 'stair turret' foundations are not constructed radially off the
junctions of the polygon, but square from the facades of the bay walls,
and such a procedure would account for this nearer stair turret being rotated
slightly away from the viewer. It would also account for the oblique visibility
of the facade of the right-hand stair turret, since it, for the same reasons,
would be rotated off the radial towards the viewer.
I believe the attention to detail (roof tiling, shading) around this turret
is due to three factors: the turret is central to the building as sketched
and its highest point is precisely marked (possibly by topographic sighting);
it is angled away from the viewer sufficiently to enable the sketcher to
give a good account of it three-dimensionally; and it is a key to other
features, since it provides secure starting-points for the curved roof-lines
(B, C, D) of the main structure. For these reasons I believe that this nearer
stair turret should be taken extremely seriously and placed high in a hierarchy
of reliability in the sketch, in contrast to the anomalous sections in the
sketch which will occupy us below. The sketch features two versions of the
right-hand stair turret, representing different initiatives from the pencil
phase of the process. There have been at least two attempts (A, B) to create
the curve of the polygon's roof on the far side of the building. The higher
of these two lines is much heavier than the lower one. This higher line
terminates abruptly where it runs into a crease-line in the paper (H), and
it is from this termination-point Hollar has made a first attempt to sketch
the stair turret's roof ridge, gable-line and flagpole (J). A subsequent
decision to privilege instead the lower of the two curving roof-lines has
led to this first version of the turret being abandoned in favour of a re-drawing
of the stair turret (K) lower down, aligned with the lower of the two curving
roof-lines.
This second, completed version of the right-hand stair turret has then
been 'sacrificed' in the third, inking phase of the process. As Hodges suggested
(Gurr et al, 1993: 12-13), a pencil-mark indicating the right-hand extremity
of the polygon (L) has been ignored, and a new ink line (M) added to its
right, resulting either in an impossibly shallow stair turret, or one that
is further away from the viewer, its side obscured by the intervening curve
of the polygon. The massive superstructure of the stage cover seems well-integrated
into the geometry of the polygon, as indeed it must have been to achieve
and maintain structural rigidity; the structural issues involved will concern
us below. However the M-shaped double gable of the stage cover is inaccurate
if it represents a symmetrical structure: the nick or 'v' between the two
faces of the gable is not centred, which has the effect of unbalancing the
facade and making the farther half of the M seem larger than the nearer
section. The lines down to this central valley (G) are manifestly tentative:
they seem to have no underlying pencil-line, and the slight bifurcation
evident in the nearer component is the result of a tentative inking, then
revised. In addition, at the left-hand end of the nearer ridge the two pencil-lines
cross and 'overshoot' each other at the point of intersection (Q)—clearly
they have not been drawn to a topographic sighting mark, but have instead
been sketched. This is an important intersection (the 'top-left' corner
of the building), and if such a key datum is the result of sketching rather
than of topographic sighting one must seriously question Orrell's interpretation
of Hollar's technique.
Visible in the valley between the two roof-ridges is the problematic 'onion
dome' (N). It is generally assumed to represent a lantern (and has been
transformed into one in the final etching), but its positioning is mysterious.
It is unlikely that its principal function is ornamental, since it is on
the southwest side of the building, obscured from most points of view on
the north of the Thames by the stage-cover ridges; its positioning in the
valley between the roof ridges suggests it must have been of significant
practical import, since it would have caused major drainage problems in
wet weather. It will be suggested below that it served the important function
of providing light to the back part of the stage, and this has ramifications
for the shape of the stage that might be inferred by the structural considerations
to be developed below. A further problem is created by a diagonal line under
the right-hand side of the dome (O). Hodges (Design 13) understood it to
be part of the dome structure (symmetrical with a similar line which seems
to mark the dome's left-hand underside). Once again discussion below, based
on the CAD research, may throw light (or rather shadow) on this line. Before
progressing to an interpretation of what structural principles might underlie
this unusual combination of architectural elements, it is necessary to address
the question of the archaeological remains: how any such intuited structure
would have sat on those remains will determine how it would look from Hollar's
point of view, and such considerations will constrain our interpretation
of the sketch and the form the basis for our design choices.
The archaeological data and assumptions about the
Globe
Since the uncovering of important archaeological evidence in 1989, we are
able to discuss somewhat less conjecturally than previously what the footprint
of the Globe was. If we accept the assumption that the first and second
Globes shared the same foundations, these remains are invaluable, enabling
us to project various possible polygonal configurations and the structural
relations to the polygon of the ancillary structures (stair turrets), and
to establish the exact position and elevation of the building in relation
to Hollar's point of view. The bay uncovered in the 1989 excavation has
been the subject of serious discussion and not inconsiderable disagreement
(Gurr et al, 1993: 20-52, 107-15). Its walls and junctions are sufficiently
ill-defined as to permit a variety of dimensional interpretations, but precise
enough to enable the elimination of a number of previously-championed configurations.
It led to the definitive rejection of the 24-sided playhouse previously
supported by Richard Hosley and John Orrell, and to the physical construction
of a 20-sided 100' playhouse.
My 1996 article suggested that one configuration not considered previously,
a 16-sided 86' playhouse, has a bay which is close in dimensions to a bay
of a 20-sided 100' playhouse, and is compatible with the archaeological
evidence. John Orrell's 1998 response to those claims is substantially taken
up with a trigonometrical demolition of that proposition and in particular
of a figure there which superimposed a notional bay on the archaeological
remains. However Orrell's formidable trigonometry has been deployed against
a paper tiger, as he could have easily verified by contrasting that figure
to Figure 4 below, which corrects the error—a correction he had already
seen in a draft of an earlier article (Fitzpatrick, 1999). The slight error
at the northern end of the projected bay in the earlier figure was caused
by volatility in the computer graphics software used, a misalignment which
an alternative software package has corrected.
In Figure 4 computer-aided design software (rather than computer graphics
software) has been used to generate the lines and angles of the bays with
a high degree of accuracy, and the figure also contains, in addition to
the original scale-bar (which Orrell correctly suggests has been rendered
inaccurate due to distortions in the reproduction process), a scale-bar
which indicates the true scaled sizes of the bays superimposed on the small-scale
image. This scaling has been derived from a close examination of the ACT
89 large-scale drawing kept in the Museum of London Archaeological Service
archives, which has enabled me to validate in particular that the diagonal
measurement across the bay (i.e. the distance between its the SW and NE
corners, a figure derived geometrically: 18'11" for a 16-sided 86'
ad quadratum polygon) corresponds to the real distance between the
relevant features of the archaeology as preserved in the original drawing.
Figure 4 indicates, pace Orrell's views to the contrary, that a 16-sided
86' configuration is not incompatible with the archaeological findings.
This superimposition does not, as Orrell argues, make the bay's northern
wall stand "altogether clear of the northern crosswall" (7), and
neither does it make the 'stair turret' an "almost improbably squiffy
[sic] affair" (6):
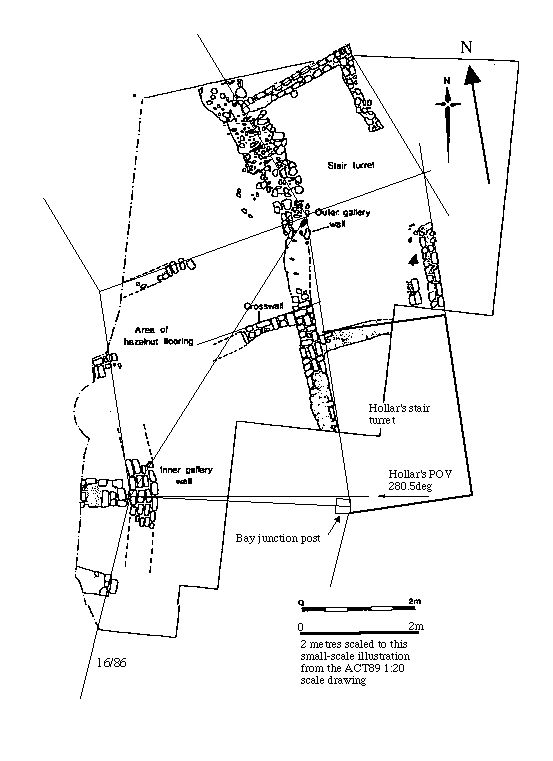
(Figure 4. A 16-sided 86' ad quadratum bay superimposed on the archaeological
remains)
Figure 4 also contains important other information: the survey data indicates
that the relationship between the excavated wall junctions and Hollar's
point of view atop the tower of Southwark Cathedral is as follows: Hollar's
line of sight from the tower to the inner wall junction runs at 280.5 degrees
from true north (i.e. he was looking slightly north of west at the centre
of the playhouse). Now since the radial of the polygon that would bisect
the two arms of this inner wall junction (i.e. would form the southern side
wall of the excavated bay) runs at very close to this bearing (at around
283 degrees), it would seem that this excavated bay happens to be the very
section of the playhouse which lies closest to Hollar's point of view atop
the tower of Southwark Cathedral. It is precisely for this reason that Figure
4 also includes a conjectural 'Hollar's stair turret', to indicate the putative
position of the nearer of Hollar's two turrets. If this bay is the one closest
to Hollar's point of view, then the turret which he draws almost at the
centre of his sketch of the building (see below) must have been attached
just here to the polygon. Such a suggestion is consonant with a further
insight derived from the archaeology: the relationship of ancillary or lean-to
structures to the polygon. The so-called 'stair turret' remains unearthed
around the outer bay junction, though wrongly positioned (and too wide)
to represent the foundations of either of Hollar's turrets, are a clue that
such structures would have been built at bay junctions rather than on the
mid-line of the bay as had previously been assumed by Hodges and Hosley.
The excavations show no indications of foundations of a mid-bay turret on
this bay facing Hollar's point of view, so the inescapable conclusion is
that if Hollar was in any way accurate in his placement of the stair turret
it must have been on the southern end of the bay in question, perhaps sharing
a foundation wall with the other excavated lean-to structure. The right-angled
rather than radial connection to the polygon (as shown in Figure 4) would
make the stair turret angle away from Hollar's point of view by approximately
10 degrees (depending on the number of sides to the polygon). What the 'stair
turret' excavated in 1989 might have been is not clear—perhaps it was a
single-story entrance foyer for the yard and lower gallery, providing access
as well to the upper galleries via a door in the side wall of Hollar's stair
turret.
Computer Aided Design (CAD): The new tool
If the 16/86 configuration can be accepted as not inconsistent with the
fragmentary archaeological data, can a consideration of Hollar's sketch
strengthen the arguments in its favour—and conversely can it serve to validate
aspects of the sketch? Although an interpretation of Hollar's work as a
sketch rather than a potentially accurate topographic drawing may seem to
suggest that it is of little authority (or even, as Orrell seems to suggest,
of no relevance at all: 1998, 5), this is not necessarily the case. An appreciation
of Hollar's drawing as a sketch facilitates discussion, since various features
that were frankly puzzling if it was a topographic drawing are simply explained
if it is understood as a sketch. While I believe strongly that the Hollar
sketch provides no viable basis for a calculation of the size and scale
of the second Globe, I also believe that as a sketch it may offer other
kinds of very significant information about the relationship and proportion
of the constituent elements of the original object under Hollar's scrutiny
from the tower of Southwark Cathedral (and hence of its more illustrious
antecedent). With these considerations in mind I set about the task of establishing
the extent to which Hollar's sketch, despite its sketchiness and the reservations
heaped upon it by previous scholars, might stand up to rigorous analysis.
To this end, with the invaluable assistance of Mr Russell Emerson, Technical
Director of the Centre for Performance Studies, I employed computer-aided
design (CAD) technology. This design tool supersedes in accuracy traditional
techniques of geometric projection such as those used by Hodges, and (despite
some inherent limitations which will be discussed below) enables the constructed
building to be viewed in a variety of ways from various angles.
If we made a series of assumptions about the structure and components of
the building we believed Hollar was sketching, the CAD tool would enable
us to compare precisely our preferred 16-sided 86' configuration with Hollar's
sketch, and a substantial match might be some vindication not only of Hollar's
accuracy as a sketcher, but also a partial vindication of our preferred
16-sided theoretical object as the most likely building that lay under his
gaze from the tower of St Saviour's. Our procedure would therefore be to
use CAD to build our 16-sided polygonal hypothesis, working out the locations
of the stair turrets on the polygon (on bay-junctions, and equidistant from
the building's axis of symmetry) and their relation to the stage cover (about
45 degrees around from the cover). We could then look at our building from
a particular point of view: from data supplied by Dr Bill McCann of MoLAS
we knew not only the bearing, but also the distance and relative elevation
of Hollar's point of view in respect of the excavated remains. The distance
from Hollar's viewpoint near the SW corner of the tower of Southwark Cathedral
to the inner wall junction is 1181.683', and the relative elevation is 144.357'.
Since CAD enables us not only to construct various configurations of the
building, but to rotate and view them from any particular angle, we could
build the Globe plus a line 1181'8" long emanating from the inner wall
junction but diverging by 2.5 degrees from the bay-wall radial (see Figure
4), and connect this base-line to a tower 144'4" high (and add 5' to
allow for Hollar's estimated physical stature). We would then be able to
view one part of our 'building' (the Globe) from the other part (the top
of the tower). In other words, rather than simply rotating our CAD version
of a hypothetical Globe until we found a point at which it 'looked good'
and corresponded to Hollar's sketch, we would be able to be more stringent
and lock ourselves precisely into Hollar's point of view and establish the
extent to which our theoretical object, viewed from his position atop the
tower, corresponded to his sketch. If there were significant correspondence
we would be able to argue that the two artifacts validate each other.
Any attempt to get closer to an understanding of the structure and layout
of the building which Hollar was sketching must necessarily make a number
of assumptions, and it is important that the assumptions we have made be
spelt out in advance. Firstly we assumed that the stage cover Hollar sketched
was a symmetrical structure, the obvious asymmetry of the facade resulting
from inaccurate sketching as C. Walter Hodges argued in 1973 (42). We therefore
assumed that the axis of symmetry of the stage cover and stage lying under
it is represented (though slightly inaccurately) by the valley between the
two ridges, the central 'nick' of the M-shaped double gable. We also assumed
that, whatever the number of sides to the polygonal drum, the two stair
turrets were located symmetrically on its circumference in relation to this
central axis of the playhouse as defined by this orientation of the stage
cover. Further, we assumed that this stage cover was attached to structural
elements of the polygon proper, i.e. to the existing bay junction posts
on both the outer circumference (at rear) and on the inner circumference
(at or near the downstage line, as argued by Hodges, 1973: 42), rather than
being geometrically and structurally independent of the polygon. We also
assumed that the second Globe had no jetties (since they had been outlawed
in 1611: see Orrell, 1983: 122), and that therefore the resultant shallower
upper galleries might not have needed to be as high as those specified for
the Fortune; for this reason we settled on galleries of 12' (1' footings
+ 11'), 10' and 8' for a structure 30' high to the eave-line, or 3' lower
than the Fortune.
Initially we built a rudimentary M-shaped stage cover, a computer graphic
equivalent of a piece of paper folded into an 'M' which mimicked the 'skin'
portrayed by Hollar. It was designed to be anchored on four posts of the
polygon proper as suggested above (and discussed in detail below), but at
this point we made no attempt to understand the structural principles which
might lie beneath the shape of the cover itself. This 'origami' cover and
the stair turrets were attached to the CAD drawing of a 16-sided polygon.
As noted above (Figure 3) in Hollar's sketch the angle between nearer stair
turret and stage cover (a), and that between the two turrets (b), seem to
be respectively in the 40-50 degrees and 60-80 degrees ranges, so the stair
turrets were placed two bay junctions or 45 degrees around from the downstage
line, with the result that the angle between the two turrets' alignments
was 67.5 degrees (i.e. both within the ranges specified). This was the result:
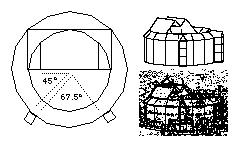
(Figure 5. 16 sided 45-degree/67.5degree with the main axis running
through a bay-junction)
As we can see immediately, this configuration demonstrates that Hollar's
treatment of the stair turrets is, pace Hodges, not to be dismissed
outright. Though they are separated by a quarter of the circumference of
the polygon, their square-on rather than radial attachment to the bay junctions
rotates each of them towards the other, enabling both their facades to be
visible. The nearer one is indeed rotated slightly away to the viewer's
right to show the side of its roof, and the right-hand turret shows its
facade obliquely, just as Hollar's inking suggests. The illustration here
is minimally larger than Hollar's original, indicating both that it is possible
to discriminate angles between the building's components even at this small
scale, and that Hollar's miniature sketching technique is possibly excellent.
Given that this exercise not only contradicted Hodges' redrawing of the
right-hand stair turret, but also reinforced the viability of our hypothetical
object and provided evidence of convergence between it and Hollar's sketch,
we began to build our CAD object in more detail. The most complex of the
structural issues to be addressed was that of the geometry and integration
with the polygon of the stage cover: if we were undertaking the CAD construction
of a coherent and integrated building we would need to find a logic and
rationale behind the relationship between polygon and stage cover as portrayed
by Hollar. Where and how might the cover have been connected to the polygon,
what was its underlying structure, how was its span supported, and could
such considerations lead us closer to certainty that Hollar might have been
sketching with some accuracy one particular polygon with a structurally
viable stage cover attached to it at four logical points? We have noted
above the apparently rectangular structure of Hollar's stage cover and the
probability that at the rear it is anchored to the outer ring of the polygon,
while its front facade seems anchored to the inner perimeter of the polygon.
If we consider our 16-sided ad quadratum construction (Figure 6),
it is easy to see where such anchor-points would be: there are four posts,
two on the outer ring and two on the inner ring of the polygon, which, thanks
to ad quadratum geometry, are in a rectangular relationship to each
other.

(Figure 6. An ad quadratum ground plan, showing four potential anchor-points
for a stage cover.
But how would you build such a cover? It would obviously be impossible to
span the more than 60' across the yard with a single triangular truss, which
would put intolerable lateral stress on the polygon. Hollar's sketch indicates
that the solution adopted was more complex: the M-shaped double-gable structure
we see portrayed there is in reality better described as two overlapping
triangular or inverted 'V' trusses (Figure 7).

(Figure 7. Two triangular or inverted 'V' trusses)
But what would lie under the trusses, how would they be supported, and what
is the starting-point of the design? If we examine Figure 8 we see that
one logical starting-point for any attempt to span this void would be one
bay back from the front of the stage (that is, the thick dotted chord ab).
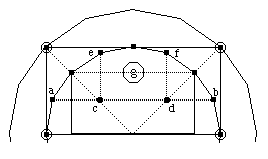
(Figure 8. The geometry of a possible stage cover supported by two stage
posts)
Two overlapping triangular trusses along this line could be supported by
posts at points c and d on the stage. Hodges (1973: 55, 64-5) noted the
key importance of the beam one bay back from the diameter or downstage line,
but argued less than convincingly that this massive superstructure could
have been supported without stage-posts. If these stage-posts are positioned
as indicated here, at the intersection of the chord ab and the radials marked
as thin dotted lines, they would also (thanks to ad quadratum geometry)
create a rectangle with two posts on the inner ring of the polygon, e and
f, further reinforcing the rectangular structure. This possible positioning
of the stage-posts is the first element in the jig-saw of the stage and
its size and shape. With stage posts positioned thus we would end up with
a central truss across the roof, one bay back from the downstage line, such
as that shown in Figure 9.
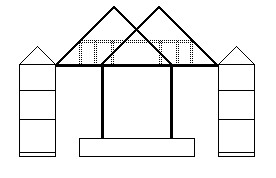
(Figure 9. A central roof truss one bay back from the downstage line)
A logical next step would be to add a horizontal 'collar tie' (to stop
the roof as a whole splaying laterally and collapsing downwards) about one-third
of the vertical distance between the main beam (a beam more accurately termed
the 'bottom chord') and the apex of the roof. Elizabethan use of quadrilateral
roof-framing has been discussed by Stuart Rigold (1981: 122, 125), and we
have adopted a number of vertical 'queen-struts' linking these two horizontal
beams (they also act, and help the collar tie to act, to prevent the diagonal
raking beams or upper chords sagging inwards). These struts and the collar-tie
are shown as dotted lines. A similar truss would be employed at the rear
end of the roof, whereas at the front gable a lightweight truss would suffice
(see Hodges, 1973: 64-5) since most of the weight would be taken on the
other two trusses, supported mid-span by the stage posts c and d and the
posts e and f. The elimination of the bottom chord and the lower sections
of the inner raking beams on the front truss (the dotted lines in Figure
10) creates a gable such as that clearly visible in Hollar's sketch. This
raising of the 'ceiling' at the downstage line would also allow more light
onto the stage. Both these front and rear trusses would be spanning a slightly
wider distance than the central truss, so their outer raking beams would
be slightly longer and meet the polygon lower down on the four anchor-points
at the corners of the stage cover, as can be seen in Figure 11.
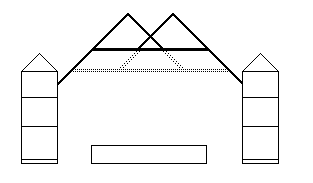
(Figure 10. Elevation of the front roof truss, spanning the full width of
the yard and meeting the polygon lower down than the central truss)
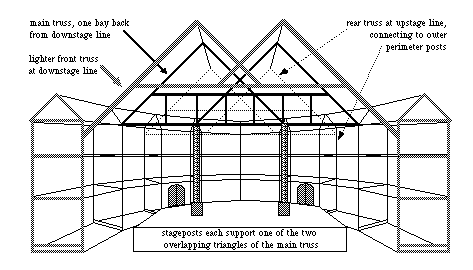
(Figure 11. The three trusses, the stageposts and the connections to the
polygon)
This object, a revised version of the first, which now took into account
these complex structural considerations around a stage cover integrated
with the polygonal drum, was then constructed using Minicad CAD software,
and the resulting image superimposed on Hollar's sketch. The result is shown
in Figure 12.

(Figure 12. Outline of CAD object superimposed on Hollar's sketch)
Once again, this image of the CAD object is viewed from Hollar's point of
view, not from a point of view chosen because it would enhance the 'fit',
and again one is struck by the significant correspondences. It shows (in
blue) the front truss and its collar tie; behind it under the roof are plainly
visible (highlighted in green) the diagonals of the main truss (this image
does not include the detail of the queen-struts discussed above).
However there is one notable discrepancy which led to the next phase of
the project. The two parallel ridges of the stage-cover, in comparison to
Hollar's image, kick up to the left. This is due to a CAD software limitation:
its orthogonal projection shows accurately the size of a building's components
so exact dimensions can be measured from the projection, despite the fact
that they may be at different distances from the viewer (so that under normal
circumstances perspective distortion would make the one further away look
smaller). This means that the left-hand end of the stage cover is shown
as the same size as the nearer or right-hand end, and causes the ridge to
kick up in comparison to Hollar's rendition of the building (which incorporates
perspective distortion to reflect the building as he sees it from his point
of view). Accurate perspective projection (with the capacity to specify
a particular distance from point of view to object) would overcome this,
but our software did not have such a facility.
Construction of a physical model
Prompted both by the fact that the correspondences with Hollar's sketch
were so remarkable, and by the limitations of the CAD software in regard
to perspective distortion, we immediately took the next logical step of
building, on the basis of our CAD plans, a 1:50 scale model of our building.
Yet again we were able to view and capture the physical model from the precise
angle and scaled distance and elevation of Hollar's point of view. The multiple
image in Figure 13 shows the model and, superimposed on Hollar's sketch,
a computer-generated line-drawing of the model.

(Figure 13. A 1:50 card model of the 16/86' Globe photographed from Hollar's
point of view, with a line-drawing of the model superimposed on Hollar's
sketch)
We believe that the correspondence between the model and Hollar's sketch
is startling, and one notes immediately that the parallel ridges of the
stage cover are now much more closely aligned with Hollar's. Note in particular
that the stage cover as we have designed it enables us to see in under the
collar-tie some of the infrastructure of the main truss one bay back from
the downstage line. This infrastructure is represented in Hollar's sketch
by a number of vertical lines, possibly representing the queen-struts from
the major horizontal beam up to the collar tie as shown in Figures 9 and
11. This exercise provides one additional insight: when it is lit by morning
sun so as to recreate Hollar's shading on the polygon to the right of the
nearer stair turret, we see one possible explanation for the line O (Figure
3) in Hollar's sketch. The diagonal line below and to the right of the onion
dome, considered by various scholars to mark the under-side of the dome
or the (incorrect) far gable of the further ridge of the stage cover, may
instead have been drawn by Hollar to mark the shadow-line created by the
dome on the roof below it.
It is also necessary to comment on the location and function of the onion
dome, and in doing so we come to another factor which impinges on the possible
shape and size of the stage in this playhouse: in the model the location
of the onion dome is indicated by the polygon g in Figure 8. It is clearly
at least partly behind the chord that would represent a straight tiring-house
wall, and since it would serve no useful purpose in providing light to the
tiring house (which could easily have windows on the outer walls of the
polygon proper) we can only conclude that its main function was to provide
light via a light well to the back of the stage, and that the stage therefore
was deeper than usually thought, going back to a concave tiring-house wall
which followed the cants of the polygon (as at the Rose: see Bowsher, 1998:
39, 50) rather than a straight wall such as that de Witt shows us at the
Swan. The gloom cast over the stage by such a massive cover might well have
provided sufficient motivation for the construction of a lantern in the
valley between the two ridges, in a location that would surely have been
problematical as far as drainage was concerned. Hodges rightly argued in
1973 that this curious superstructure must have had a serious function to
be placed in such a problematical position (1973: 73-4). He too located
the lantern forward and clear of the polygon in a position very close to
that validated by our CAD design (43).
However there are a number of discrepancies between the model and Hollar.
First, the M-shaped gable of the stage cover: the model corresponds precisely
with the near-side line in Hollar's sketch, while the farther side of the
facade is slightly misaligned, a discrepancy easily accountable simply by
the obvious inaccuracy of the sketching at this point. The second discrepancy
concerns the two versions of the right-hand stair turret: in the light of
Figures 12 and 13 Hodges' suggestion that this stair turret should be facing
away from the viewer and requires redrawing seems unfounded, since Hollar's
inking is both logical and possible. The third discrepancy concerns the
right-hand end of the polygon: the model supports Hodges' contention (Gurr
et al, 1993: 12-13) that the pencil line (L) in Figure 3 is a more accurate
marker of the right-hand extremity of the polygon, and is therefore to be
privileged over the ink line (M). The final and most significant mismatch
between the model and Hollar's sketch concerns the height to the eave-line
of the polygon. Our superimposition of the model on Hollar's sketch provides
no indications of absolute dimensions of the latter: all our discussion
has been about the proportion and configuration of the elements of the building
as sketched by Hollar. We can say that the superimposition of the 86' CAD
structure we have built on Hollar's sketch evidences a mismatch at ground-level.
Our building is, as indicated above, 30' to the eave-line, and it still
'goes underground' in respect of even the lowest of the pencil-lines, hidden
in the bushes, that Hollar has marked as the base of his building.
This discrepancy, while not directly disqualifying a 16-sided polygon,
would nevertheless seem to disqualify one as small as 86' (and the bay excavated
in 1989 would seem to preclude a 16-sided playhouse of larger dimensions).
Is there any possible explanation for this discrepancy? Perhaps there is
if we return to the insight advanced by John Orrell in regard to some of
Hollar's other drawings: that after topographically locating buildings in
his panorama, he then sketched and enlarged them, bringing them into greater
prominence in the surrounding townscape. Orrell queries the accuracy of
Hollar's sketching of other parts of London, and cites discrepancies between
accurate position and inaccurate scale in another of Hollar's topographic
drawings, 'London and Old St Paul's from the Thames':
We must notice that there are limits to its accuracy. For one thing, the skyline seems too neatly arranged as a set of towers and spires, many of which appear to out-scale their surroundings. For another, the lantern on Middle Temple Hall seems over-large, leaving doubts about other details of the view. What the artist has got abundantly right are the intervals between the major landmarks: these are presented with all the accuracy of a topographical survey, while the details of the view are subject to the artist's interpretive vision. (1983: 19)If Orrell had applied such an important insight to this sketch as well as to the others he takes into consideration, he might not have pursued so relentlessly a trigonometrical approach to this one particular sketch. This important insight provides the basis for the substantial re-interpretation of Hollar's sketch undertaken above, and it can be argued that the Globe he has sketched exemplifies perfectly the discrepancy Orrell notes between accurate location and inaccurate scale. There are possibly certain key pencil marks based on a limited number of topographic sightings taken to locate the building in the panorama, but the artist has then created multiple versions of it, trying out various sizes in pencil—and then, in the first 'redrawing', inking only one of them.
If this is indeed a sketch rather than a fully topographical drawing, then
the process would have had at least three distinct phases: firstly the artist
would mark some key high-points on the building using the topographic glass
or frame (e.g. the ends of the roof ridges, the points of the stair turrets,
the peak of the onion dome); secondly, having transferred those marks to
his paper, he would sketch the rest of the building freehand in pencil (at
some points providing himself with multiple choices); and thirdly he would
'redraw' it, inking over some of the pencil-marks to create the finished
ink drawing. This redrawing would involve both choice (which of the multiple
pencil-sketch marks are to be inked?) and memory--since for purely practical
reasons this final phase of the process would most probably take place back
in the artist's studio, and could thus be the site of inaccuracies.
There is one important corollary of such a suggestion: any 'scaling up'
by Hollar of the prominent landmark buildings in the panorama, once located
accurately by the sighting technique, would normally take place outwards
and downwards from the topographic sightings of the building's high-points
to which his technique committed him. We will literally never get to the
bottom of the sketch if Hollar was indeed systematically enlarging the building
as he proceeded with pencil and pen, stretching it outwards and 'driving
it underground'. This outwards and downwards enlargement might well be exemplified
by the three pencil lines (S) in Figure 3 which tentatively mark various
possible baselines for the polygon, and the bushes which hide our view of
this baseline may have been Hollar's means of avoiding a commitment to a
definite vertical dimension for the horizontally-enhanced building he was
sketching. We might also note in this regard that the ridge-line of the
roof of the building immediately in front of the Globe (see Figure 2) has
been lowered substantially in the inking phase, perhaps to maintain intact
the proportion of the visible part of the Globe.
Conclusion
Works Cited
Bowsher, Julian (1998). The Rose Theatre: An Archaeological Discovery. London: Museum of London.
Fitzpatrick, Tim (1989). "The Dialectics of Space-Time: Dramaturgical and Directorial Strategies for Performance and Fictional World". In T. Fitzpatrick (Ed.), Performance: from Product to Process. Sydney: Frederick May Foundation, 48-111.
-----. (1995). "Shakespeare's Exploitation of a Two-Door Stage: Macbeth". Theatre Research International, 20.3, 207-30.
-----. (1996). "The Fortune Contract and Hollar's Original Drawing of Southwark: Some Indications of a Smaller First Globe." Shakespeare Bulletin, 14.4, 5-10.
-----. (1999). (with Russell Emerson), "Reconstructing the spatial dynamics of 'lost' theatre spaces: Shakespeare's second, first and third Globe Theatres". People and Physical Environment Research, 53-54, 42-57.
Gurr, Andrew (1992). The Shakespearean Stage 1574-1642. Cambridge: Cambridge University Press.
Gurr, Andrew, Mulryne, R. and Shewring, M. (Eds) (1993). The Design of the Globe. London: International Shakespeare Globe Centre.
Hildy, Franklin J. (Ed.) (1990). New Issues in the Reconstruction of Shakespeare's Theatre. New York: P. Lang.
Hodges, C.W (1973). Shakespeare's Second Globe: The Missing Monument. London: Oxford University Press.
Hosley, Richard (1981). "The Shape and Size of the Second Globe". In C.W. Hodges, S. Schoenbaum and L. Leone (Eds), The Third Globe. Detroit: Wayne State University Press, 82-107.
Kemp, M. (1990). The Science of Art: Optical Themes in Western Art from Brunelleschi to Seurat. New Haven: Yale University Press.
Orrell, John (1983). The Quest for Shakespeare's Globe. Cambridge: Cambridge UP.
-----. (1993). "The Accuracy of Hollar's Sketch of the Globe". Shakespeare Bulletin 11.2, 5-9.
-----. (1998). "The Size and Shape of the First Globe: Interpreting the Archaeological and Mathematical Evidence". Shakespeare Bulletin 16.3, 5-8.
Rigold, S.E. (1981). "Appearance and Reality: A Carpenter's Viewpoint". In C.W. Hodges, S. Schoenbaum and L. Leone, (Eds), The Third Globe. Detroit: Wayne State University Press, 117-135.
Responses to this piece intended for the Readers' Forum may be sent to the Editor at m.steggle@shu.ac.uk.
![]()
© 2004-,
Matthew Steggle (Editor, EMLS).