-
In the late 1990s, rhetoric over attributional methodology
reached a boiling point in the journal Computers and the Humanities.
Political scientist Ward Elliott and mathematician Robert Valenza, both
of Claremont McKenna College in Southern California, presented results from
a massive battery of computerized tests comparing the Shakespeare canon
to a phalanx of Shakespearean claimants. Even though their Claremont Shakespeare
Authorship Clinic had hoped to validate an anti-Stratfordian claim (that
Edward de Vere was the “true” Shakespeare), the results they reported showed
quite the opposite – that Shakespeare, whoever he was, was not any of the
other writers examined in the study. His signature style stands out, unique,
implicating the man from Stratford by process of elimination.
-
It was a result that most Stratfordian scholars must have
been pleased to see. Yet Don Foster, the Claremont project’s erstwhile literary
advisor, penned an article for the same issue in which he argued against
the clinic’s results and methodology, contending that works compared by
the Claremont team were not consistently edited;
[1] that several tests were redundant;
[2]
that the clinic failed to control for chronology;
[3] that its test results cannot be replicated due
to under-reported information;
[4] and that, due to miscounting, the clinic’s figures “are wrong
so often as to be worthless.”
[5]
It was an eye-catching response, coming from a former advisor to the project
– and a Stratfordian. However, in returning fire, Elliott and Valenza noted
that their opponent’s attacks focused eight out of ten times on tests that
had undermined Foster’s Shakespearean attribution for
A Funeral Elegy,
suggesting ulterior motives.
[6]
-
The resulting war of words, spanning six years, did not
go well for Foster. Scholarly opinion has tended to support the clinic,
with the conservatively inclined Brian Vickers ultimately taking sides with
the one-time Oxfordian scientists.
[7]
Moreover, on the heels of an article by Gilles Monsarrat, and shortly before
the publication of a similarly-themed book by Vickers, Foster eventually
conceded that John Ford, rather than Shakespeare, probably wrote the
Elegy.
[8]
-
Nevertheless, Foster has not retracted his accusations
against the Claremont clinic. Vickers has defended Elliott and Valenza,
but even Vickers does not trust some of the tests that the team borrowed
from earlier attributionist A.Q. Morton,
[9]
and he has attacked Foster for using techniques based on sentence length
[10] that the Claremont clinic has
also used. Other Shakespeare scholars also have some reservations about
some of the clinic’s methods. When Joseph Rudman published an article on
the state of attribution methodology shortly after the initial Claremont-Foster
fracas, his lessons echoed many of Foster’s complaints.
[11] David Kathman, meanwhile, has contended that the Claremont researchers
“rely too heavily on the results their computers give them, using a program
to crank out a ‘yes’ or ‘no’ result rather than using the computer's results
as one type of evidence in a comprehensive attribution study.”
[12]
-
What, then, are we to make of the study and its methodologies?
Which, if any, of the clinic’s results can be trusted, and what sorts of
conclusions can we draw from them? This paper aims to answer these questions.
-
A study of this sort is important for several reasons.
First, if the bulk of the Claremont figures are valid, scholars might have
to rethink their attributions of works like
Edward III and even,
as will be discussed at greater length below,
Edward II. Second,
if the figures are at all useful, they provide us with a trove of data,
ripe for secondary analysis simply because the study was so sweeping in
its scope. Third, the validity of the clinic’s tests and methods has ramifications
for more than just questions of authorship. If the tests are valid, they
might help answer other questions about our favorite authors, beyond whether
any of them wrote a particular poem. For instance, such methods can be used
to study the influence one author has had on another, as demonstrated by
Thomas Merriam’s study of Marlovian word choice in Shakespeare’s early history
plays, based in part on software from the Claremont clinic.
[13]
Similarly, MacDonald P. Jackson’s computer analysis of Ants Oras’ 1960 pause
pattern study provides us with a way to check the accepted chronological
placement of play-composition dates.
[14]
Accurate attribution also matters to scholars interested in biography and
the history of texts. Kathman, in an online debate over authorship of the
Elegy, once answered a bystander’s question query of “What does it
matter?” by noting that “The Funeral Elegy is a very personal poem, and
if Shakespeare did write it, that fact has enormous biographical significance.”
[15] In short, any authorship attribution study has a host of ramifications
for scholars.
-
The discussion below will summarize and evaluate critics’
objections to the Claremont study as they apply to plays (I am setting aside
discussions of nondramatic poetry for this paper), weed out tests that seem
unreliable, make a note or two about methodology, and construct a secondary
study based on the surviving tests. The purpose of this secondary study
will be quite different from that of the Claremont clinic. Because the issue
of Shakespearean claimants appears largely settled, I wish to use the revised
data to collect evidence on which plays probably belong in the Shakespearean
canon, which might be considered suspect, and which plays presently outside
the canon might be due for closer examination. The results in most cases
support expectations that have been built up over many years of qualitative
scholarship, and thus largely function as a quantitative endorsement. However,
the statistics also suggest some new questions. They suggest that something
is amiss, either in the attributional methods being used, or else in our
understanding of what Shakespeare wrote.
A Review of the Claremont Study
- Several of Foster’s complaints can be dealt with swiftly, namely the accusation
of inaccurate counts and a later charge that the clinic silently altered its
data between reports.[16]
Since Foster’s attacks, Elliott and Valenza have obligingly corrected several
errors, but ultimately the errors have been few and insignificant – correcting
them has had no impact on the clinic’s conclusions. Most of the other supposed
miscounts they have aptly covered with the following rejoinder, which suggests
it is Foster who needs to recalibrate his fingers:
Our published figures are standardized to rates per 20,000
words and are clearly and repeatedly so described; for example, see
our 1996, pp. 200, 222, and 224; our 1998/99, p. 436. Despite all the warnings,
Foster has persisted in reading them as if they were raw numbers and then
telling us, erroneously, that we have miscounted.[17]
Vickers finds their rebuttal persuasive,[18]
and so do I. We also seem to agree[19]
that updating data is acceptable, even commendable, if handled in the fashion
described by the Claremont researchers:
[O]ur “silent and extensive alteration of data” and our “suppression”
of weak or redundant tests are […] exactly what you should expect to happen
if you continue to recheck data, look for errors, redundancies, imprecisions,
and inconsistencies, and correct them – and if, as is looking more and more
likely, the tests are good. We did this rechecking relentlessly throughout
the Clinic, went on doing so long after the Clinic closed down, and shall
doubtless continue to do so […].[20]
Data errors are inevitable, but few professionals are
courageous enough to fix them in the spotlight. Foster’s observation, designed
to undermine confidence in the Claremont figures, if anything has had the
opposite effect on me. I suspect, though of course I cannot be certain,
that the Elliott and Valenza counts are more accurate than most. This is
not the same thing, however, as believing that their tests are measuring
what they say they are measuring. We must still deal with charges that the
tests themselves are invalid.
Mulling the Modal Tests
-
Foster poses many challenges to the Claremont clinic’s
original, signature battery of tests, particularly two colorfully dubbed
measurements: Bundles of Badges (BoB) and Bundles of Flukes (BoF). By Claremont
definitions, a “badge” is a word that Shakespeare prefers more than his
peers do; a “fluke” is a word that he uses less often than his peers do.
(The clinic came up with its lists of badges and flukes by generating word-counts
for each word used by Shakespeare in a 120,000-word sample and then subtracting
similar totals of word occurrences from a 120,000-word sample comprising
other playwrights.) Assuming the counts are accurate, a Shakespeare play
should have more Bardic badges and fewer Fletcher-style flukes than other
plays of the same period do. Elliott and Valenza grouped various badges
and flukes into several “bundles” representing mini-profiles of Shakespearean
writing quirks. By counting the number of badges and flukes for each bundle,
subtracting the flukes from the badges, and then dividing that total by
the sum of badges and flukes, the clinic could get some idea of how “Shakespearean”
a work might be. By way of example, a bundle called BoB1 compares counts
of
you,
your, I, he, she, and
it (badges) to those
of
ye, thee, thou, thy, and
we (flukes).
[21]
-
Foster grants that Shakespeare prefers
you over
thou, but he thinks BoB1, BoB3, and BoB5 are largely redundant because
all three tests include that
you versus
thou showdown in their
line-ups. “[T]he authors seem unclear about what it is that they were actually
testing,” he writes, adding that “the discriminating power of each bundle
may be largely controlled by just one or two of its principal components,
with the other words providing only static.”
[22]
Although Foster did not do so, it is possible to check for signs of redundancy
by looking for abnormally high correlations, or
multicollinearity,
among independent variables. It turns out, for instance, that BoB5 is independent
enough, but that BoB1 and BoB3 are highly and significantly correlated (Pearson’s
r = 0.856, p<.001).
[23]
Although one would normally consider high correlations among several tests
desirable, a sign that the battery as a whole is reliable, we cannot draw
such an optimistic conclusion for two highly correlated tests that share
a common variable, particularly if it is difficult – as it is in this case
– to parse out the offending variable and thus gauge its impact on the level
of correlation. Prudence dictates that we treat the tests as redundant,
scoring one point for Foster.
-
Does this, however, mean that we should ignore one of
the tests? That is a difficult question to answer. Multicollinearity is
not always quite as bad a sin as Foster makes out, but it can distort figures
for some purposes. For instance, a statistician would not normally worry
about such redundancy when the statistics are only being applied within
the sample, rather than to texts outside the study. However, redundancy
among tests can be an obstacle to clarity if we hope to identify individual
Shakespearean works. For instance, suppose I identify a test on which 95%
of the core Shakespeare plays fare well, and from it I create nine new redundant
tests, adding them to the overall battery. Because the claimant plays tend
to pass or fail this block of tests en masse, while the core plays
tend to pass them en masse, the gap between “could-be Shakespeare”
and “probably not Shakespeare” jumps by roughly 10 rejections. In effect,
I have taken a single test and given it the weight of 10 tests. If you
and thou really are as powerful discriminators as Foster, Elliott,
and Valenza indicate, they might deserve to be weighted in this way – they
might actually be worth two or three tests. However, if we decide to weight
tests in this way, instead of just taking the numbers of raw rejections,
we should then go through the rest of the testing battery, identify other
tests of similar power, and weight them, too.
-
One day, ideally, tests that are not redundant, using
these same badges and flukes, would be developed in place of BoB1 and BoB3.
Until then, if we are to work with the data at hand, we should probably
disregard one of the two tests. This, too, is tricky business: the tests
in question do not overlap perfectly, so we will be sacrificing some information
with either decision. Because BoB3 seems to run into some chronological
problems that I discuss in more detail below, I have decided to keep BoB1
in my revised line-up, and to eliminate BoB3. By doing so, I reduce the
number of rejections for the two most suspect core Shakespeare plays (
3
Henry VI and
Titus Andronicus) by one each.
[24]
-
While we are on the subject of modal and bundled tests,
there are two more attacks on the BoB regime to consider, one of which influences
my decision to exclude BoB3. First, Foster challenges the contraction-counting
BoB7, believing it to be chronologically biased. His point has a solid basis:
Contractions were used with increasing frequency starting in about 1600,
but a significant portion of the Shakespeare canon was already written by
then. Hence, Shakespeare appears to use few contractions compared to Jacobean
playwrights like Middleton. Foster grumbles that the test “assigns […] rejections
to 23 of 51 Claimant plays and to 9 of 28 Apocrypha plays […] but most of
those Shakespeare rejects were written after
I’m became standard
English.”
[25] The BoB regime also comes under
fire by Rudman, who, in his discussion of methodological concerns plaguing
authorship studies, itemizes a host of problems in attribution research,
including a lack of continuity (many researchers perform a study, then move
on to other subjects), overemphasis on expediency, lack of expertise in
multiple fields, and contamination of data by printers or editors. Along
the way, Rudman chides the Claremont clinic specifically for being “led
into this swampy quagmire of authorship attribution studies by the ignis
fatuus of a more sophisticated statistical technique,” noting that “[t]he
modal analysis used by Elliott’s group is derived from signal processing.”
[26]
-
Both attacks sound serious, but let us consider them.
As it turns out, Foster’s accusation of chronological bias does not seem
to apply to BoB7 – he should have pointed his finger instead at BoB3. The
attack on BoB7 makes several errors. First, Foster misconstrues the clinic’s
methodology, missing the fact that it used a Jacobean play (
Macbeth),
not an early one, to establish its parameters for contractions. His assumption
that it would reject late Shakespeare plays seems hasty in light of this.
Second, Foster ignores the crucial point that the BoB7 test, despite being
gleaned from one play, was “
validated against the full range of Shakespeare’s
poems and play verse”
[27] so that its range encompasses both early and
late work. Third, Foster should have tested his argument by running correlations
between the dates of composition and whether plays passed BoB7. As it happens,
if there is a correlation at all between BoB7’s results and play chronology,
it is not only very weak, but of borderline significance by most statistical
standards (r = 0.17, p = 0.106).
[28]
- We have thus settled the question of BoB7, and using the same process can
ease similar fears about BoB1 and BoB5, the chronology-pass/fail correlations
of which are, though statistically significant, also fairly weak – within
the range I have defined in the above footnote. However, the correlation between
BoB3’s results and play chronology seems too substantial to ignore, providing
us with a suitable tie-breaker for the BoB1 versus BoB3 showdown mentioned
earlier. BoB3, being both redundant and chronologically suspect, is out, but
the other tests can stay. Table 1 summarizes these findings.
Table 1: Correlations of BoB 1-7 with chronology
|
Test
|
Correlation
(Pearson’s r)
|
2-tailed significance
(p value)
|
|
BoB 1
|
-0.289
|
.005
|
|
BoB 3
|
-0.442
|
<.001
|
|
BoB 5
|
0.221
|
.035
|
|
BoB 7
|
0.17
|
.106
|
|
Source: All data in tables or charts are recalculated from
figures in Ward Elliott and Robert J. Valenza,“The Professor Doth
Protest Too Much, Methinks: Problems with the Foster ‘Response,’”
Computers and the Humanities 32 (1999): 425-490.
|
- What then about Rudman’s “ignis fatuus” remark? Can signal processing formulae
be helpful in attribution studies? Rudman implies not. He observes with some
concern that another attributional commonplace, the Thisted-Efron slope test
(which, incidentally, Claremont uses), was designed to determine the probability
of finding new species of butterfly.[29] What Rudman does not acknowledge here is that
most statistical procedures are developed for a specific purpose and then
exported to other problems for which they are useful. One significant, historical
source of probabilistic insights has been gambling, the lessons of which extend
well beyond Atlantic City or Las Vegas.[30] Furthermore, one of the early
famous uses for the Poisson distribution that I use later in this paper was
to calculate the statistical likelihood of deaths by horse-kicking in the
Prussian army,[31] but today
Poisson distributions are used to calculate the odds of all sorts of other
unlikely, random events, from radioactive decay to biological mutation to
meteor strikes. Accordingly, I am inclined to overrule this objection.
Weighing Whereas/Whenas
-
In another salvo, Foster attacks the clinic for using
a test in which even one instance of either
whereas or
whenas
in a play warrants a rejection on that test, writing that “Elliott and Valenza
were advised early on that the occurrence or omission of single words cannot
rightly be viewed as evidence for or against Shakespearean authorship of
any text.”
[32] Here, it seems that Foster has
failed to understand the nature of the test in question and the methodology
behind it. Like any other test in the battery, or even the battery as a
whole, it does not produce proof – it produces evidence. Much confusion
could be avoided if readers and authors would conspire to read statistics
as the latter, rather than the former. Indeed, Foster might need to reread
one of his own arguments in support of his attribution of the novel
Primary
Colors to Joe Klein, an argument that uses similar logic: “‘Towards’
(for ‘toward’) rarely appears in Klein’s journalism, and nowhere in
Primary
Colors. And so for dozens of other badges and flukes, which when taken
together provided compelling attributional evidence.”
[33]
The key phrase in Foster’s analysis here is “when taken together,” and so
it goes for the Claremont study. In this case, the Claremont clinic is not
arguing that the presence or absence of such a word should be taken as conclusive
by itself – this test is merely one indicator among many. And it is a valid
indicator. If, as appears to be the case, nearly 90% of Shakespeare’s plays
have no instances of either of the aforementioned words, despite being long
works composed in a period when these two words were known and used by others,
then we have discovered a fairly strong fluke, according to the badge/fluke
terminology above. Taken by itself, the presence of such a word is insufficient
evidence, but that does not make it bad evidence. Since one test failure
is not a verdict but rather evidence (or else we would have to excise
Othello
from the canon!), the
whereas/whenas item is – like the others –
useful as part of a testing regime. No play will be ejected from the canon
simply because Shakespeare had an uncharacteristic moment or two (or even
three). But if a play fails a significant number of such tests, well outside
of his usual rejection pattern, one can speculate with some confidence that
Shakespeare might not have written it.
Commonalization, Editing, and the A.Q. Morton Regime
-
Yet another difference of opinion revolves around the
reliability of Claremont’s data sets. Foster contends that lack of commonalization,
lack of common editing, and other problems result in noise that renders
some of the Claremont test results unreliable.
[34]
Rudman, in apparent reference to the Claremont clinics, chastises practitioners
who resort to expedient copy texts, knowing as they do so that their data
set might be flawed.
[35]
These arguments suggest that what we are detecting is not common authorship
but common editorship. That is, the plays in the
Riverside Shakespeare
plays might pass, not because Shakespeare wrote them, but because the editors
of the
Riverside Shakespeare edited them. From such edition-oriented
tests, we might safely conclude that Middleton’s plays were not edited in
the same way as Shakespeare’s, but that is not a very helpful conclusion.
-
For their part, Elliott and Valenza respond that they
did commonalize their data sets, at least, as far as spelling. However,
they stayed away from repunctuating, having noted that Foster, through aggressive
editing, managed to increase
A Funeral Elegy’s sentence length by
44% and “more than double its percentage of run-on (enjambed) lines.”
[36] Elliott and Valenza claim they wanted to avoid
such tampering. The Claremont response gives us good reason to trust most
of their tests, as many of their approaches are based on words, and thus
require commonalized spelling.
-
However, a handful of the Claremont tests depend on the
punctuation. Four tests, developed by stylometrician A.Q. Morton, depend
on the placement of words in a sentence: one test counts how often
it
is the first word in a sentence, another counts how often
it is the
last; a third test counts how often
with is the penultimate word
in a sentence, while a fourth makes an equivalent count for the word
the.
In all of these cases, the dependency on sentence placement equates to a
dependency on the provision of final periods. Moreover, the clinic’s grade
level test is based on sentence-length, and a sixth test is based on hyphenated
compound words (HCWs).
[37] What of these punctuation-based
tests? Can they be trusted? Many Renaissance scholars think not. Vickers,
for instance, has deplored Morton’s influence in the 1980s as “unfortunate”
and “largely discredited.”
[38]
Foster finds the grade level measurement particularly troubling, for instance,
since “some editors will allow sentences to run on in a good Elizabethan
manner
[39] while others curtail long sentences
with end-punctuation.”
[40]
Jonathan Hope tells us that serious difficulties “arise when Morton’s techniques
are applied to early Modern texts (not the least of which is how to define
the sentence in texts punctuated in the printing house).”
[41] In their compendium, Wells and
Taylor specifically indict the sort of sentence-based tests used by the
Claremont clinic as “impossibly inexact when applied to the modern punctuation
in (variant) modern texts of Shakespeare.”
[42] Morton himself claims his punctuation-based tests should not
be used when “the punctuation of the texts is not to be relied on,”
[43] and this certainly appears to be the case with
Renaissance texts.
-
Indeed, if scholarly consensus is correct and the Hand
D of
Sir Thomas More is in Shakespeare’s own handwriting, then we
have fairly clear evidence that he did not punctuate his own text much at
all, instead leaving spaces between words where punctuation would later
be added by other writers who sometimes, not knowing what Shakespeare intended,
appear to have erred in their punctuating.
[44]
While it might be tempting to dismiss the Hand D evidence on account of
its poor performance on the Claremont clinic’s tests, the sample size for
Hand D is – at a mere 1,382 words, compared to around 20,000 for most complete
plays – too small for effective testing, as both Hope
[45] and the Elliott-Valenza team
[46]
have noted. Moreover, as I will demonstrate later, the Claremont tests do,
in some ways,
support the Hand D contention. Even if the Hand D author
is not Shakespeare, his behavior remains tangible evidence that hazards
exist for those making assumptions about the hands behind punctuation in
early modern plays.
-
The Claremont team’s response to all of this is to say
that one should nevertheless resist the temptation to commonalize punctuation,
noting that “We think the hazards of such editing far outweigh its benefits.”
[47] They are very likely right,
but the evidence they cite in support of this caution suggests perhaps an
even greater caution is needed: instead of avoiding commonalization, we
might do better to avoid the sentence-based tests altogether. Indeed, in
taking a shot at Foster by showing that his editing changed results for
A Funeral Elegy, Elliott and Valenza undermine their own argument
that sentence-based counts can be compared from document to document. They
cannot have it both ways. If editing can affect punctuation-based results
by 44%, so too can failing to commonalize punctuation. Moreover, Elliott
and Valenza have admitted that “aggressive re-editing [of the works in their
study…] could double the number of hyphenated compound words” and that similar
approaches to other plays “could cut the rejection rate of the HCW test
about in half.”
[48] In defense of such tests, they reassure readers that “our comparisons
of several different Shakespeare editions have shown only moderate variation
(±20% or so from midpoint) between different editions for grade-level and
hyphenated compound words.”
[49]
-
Despite such assurances (and a 40% spread is not terribly
reassuring to begin with), I am inclined to disregard the entire suite of
punctuation-based tests. In this case, the weight of scholarly opinion appears
to be against Elliott and Valenza (even if heavyweights like Vickers sometimes
ignore their distaste for Morton tests to brandish the summarized Claremont
results at Foster), and the Claremont team’s own observations about Foster
also seem to support greater caution here. Accordingly, I have in my analysis
below discarded six punctuation-based tests and the figures derived from
them, in addition to discarding the BoB3 test, as mentioned earlier.
-
I realize that Elliott and Valenza’s system is designed
on a principle of falsification (what they term a “silver bullet” methodology),
and that this might have a role in any objection to my exclusion of seven
tests. In fairness to the Claremont authors, I will explain their rationale,
and then my reason for disregarding it here. Elliott and Valenza’s methodology
is largely Popperian,
[50]
and not at all as misguided or unusual as Foster apparently believes it
is.
[51] Their approach assumes – I think
correctly – that it is not really possible to prove that Shakespeare wrote
Macbeth. It should be possible, however, to show that he did not
write
Forrest Gump. Macbeth, with 1 rejection on the Claremont clinic’s
battery of tests, might be by Shakespeare;
Tamburlaine, with more
than 20 rejections, certainly is not. Such a methodology is a lot like an
enlightened judicial system, presuming innocence and preferring false passes
over false rejections.
-
By leaving the Morton-regime metrics in their survey,
Elliott and Valenza are essentially betting any contamination of data will
favor false passes more than false rejections. They may be correct. My instinct,
however, is that we should ignore the results until a more thorough test
can be made of Elliott and Valenza’s underlying hypothesis about the likely
effects of contamination, which seems to me to be subject to falsification
itself. The way to test that assumption is fairly simple, and has already
been conducted in part by the Claremont clinic. Run the core plays from
the electronic
Riverside Shakespeare against electronic versions
of the same core plays as edited by other scholars. Pay close attention
to the tests that are most prone to contamination by editors, such as those
based on sentence endings. Then check whether the
Hamlets of Project
Gutenberg and Chadwyck-Healy pass the test parameters identified by the
Shakespeare clinic. They ought to. If they garner rejections, then Foster
is right, and the offending tests should be left on the sidelines. If, on
the other hand, Shakespeare’s plays pass, contamination might still be an
issue, but probably not a fatal one.
[52]
-
Two-thirds of the clinic’s tests remain largely unmolested
by Foster and other critics. They include semantic bucketing (another modal
test, related to the BoB batteries), Thisted-Efron slope tests (which profile
the rates at which authors introduce new, rare, and common words), rare-word
tests, new-word tests, feminine line-ending percentages, open-line percentages,
contraction frequencies, metrical filler patterns,
I do + verb counts
(
I do weep), prefix counts (for instance, words starting with
where-),
suffix tallies,
most plus modifier counts (for instance, expressions
like
most noble or
most welcome), and adversion rates (
see,
hark,
listen). Many of the above categories are tested in
several permutations: There are five prefix tests, five suffix tests, sixteen
contraction tests (many of which have different acceptable ranges for different
periods, and are thus well-controlled for chronology
[53]), four metric filler tests, and two
I do
tests. These tests seem more durable than the sentence-based regime, and
as they are as yet largely uncontested, they will be included in the secondary
analysis that follows.
What Can We Make of The Revised Tallies?
-
The resulting rejection totals are intriguing, but it
is difficult at a glance to interpret them. Is a play with two rejections
much more likely to be by Shakespeare than one with four rejections, or
only a little more likely? Without even a tentative understanding of the
probabilities involved, it is difficult to gauge the significance of a play’s
results. To provide some sort of a guideline, I have run Poisson distributions
on the mean rejection totals for both Shakespeare and his contemporaries.
(Poisson distributions calculate the probabilities of unlikely, random events,
such as the number of meteors that might hit a given area over a stated
period of time, or the number of typographical errors one might expect per
page. They seem to be an appropriate tool for gauging how likely it would
be for Shakespeare to fail a Shakespeare test.) I used the Poisson distributions
to answer two questions:
1. Assuming that he wrote, solo,
every work commonly attributed to him, how often should we expect a play
by Shakespeare to look non-Shakespearean, with a high number of rejections,
just by chance?
2. Assuming that Shakespeare did not write
Tamburlaine or any of the other plays ascribed to other authors
from that period, how many of those plays should we expect to look unusually
Shakespearean, with a low number of rejections, simply by chance?
By calculating these figures, we can identify plays that appear to be defying
the odds by accumulating more rejections than the odds suggest they should
(if we believe them to be Shakespearean) or by accumulating fewer rejections
than we would expect them to (if we believe them to be by someone else).
-
Eliminating BoB3 and sentence-based tests produces a rejection
pattern for the core plays as seen in table 2, below. The Poisson figures
represent the probability that a single play would garner its given number
of rejections or more, based on the mean number of rejections (1.14)
for a work in the Shakespearean corpus. I have bold-faced Poisson figures
for plays that earned an unlikely or unexpected number of rejections, either
individually or in tandem with other plays. Note that Claremont excluded
some plays (Timon of Athens, 1 Henry VI, Henry VIII) from its core
line-up to keep it from being tainted by suspected collaborations, along
with several acts of Pericles and parts of Two Noble Kinsmen.
Those plays appear in table 4, under dubitanda.
|
Table 2: Shakespeare Baseline results
|
|
Play
|
Round 1
|
Round 2
|
Round 3
|
Total
|
Poisson*
|
|
2 Henry VI
|
0
|
0
|
1
|
1
|
0.681
|
|
3 Henry VI
|
1
|
1
|
3
|
5
|
0.006
|
|
Richard III
|
0
|
0
|
0
|
0
|
1.000
|
|
Titus Andronicus
|
2
|
0
|
2
|
4
|
0.029
|
|
Taming of the Shrew
|
0
|
1
|
1
|
2
|
0.317
|
|
Two Gentlemen of Verona
|
1
|
0
|
0
|
1
|
0.681
|
|
Comedy of Errors
|
0
|
0
|
1
|
1
|
0.681
|
|
Richard II
|
1
|
0
|
0
|
1
|
0.681
|
|
Love’s Labor’s Lost
|
0
|
0
|
1
|
1
|
0.681
|
|
King John
|
0
|
0
|
0
|
0
|
1.000
|
|
Midsummer Night’s Dream
|
1
|
1
|
0
|
2
|
0.317
|
|
Romeo & Juliet
|
0
|
0
|
0
|
0
|
1.000
|
|
1 Henry IV
|
0
|
1
|
0
|
1
|
0.681
|
|
Merry Wives of Windsor
|
0
|
1
|
1
|
2
|
0.317
|
|
Merchant of Venice
|
0
|
0
|
0
|
0
|
1.000
|
|
2 Henry IV
|
0
|
0
|
0
|
0
|
1.000
|
|
Julius Caesar
|
0
|
0
|
0
|
0
|
1.000
|
|
Much Ado about Nothing
|
0
|
0
|
1
|
1
|
0.681
|
|
Henry V
|
1
|
0
|
1
|
2
|
0.317
|
|
As You Like It
|
1
|
0
|
1
|
2
|
0.317
|
|
Hamlet
|
0
|
2
|
1
|
3
|
0.108
|
|
Twelfth Night
|
0
|
0
|
1
|
1
|
0.681
|
|
Troilus and Cressida
|
0
|
0
|
0
|
0
|
1.000
|
|
Measure for Measure
|
0
|
0
|
0
|
0
|
1.000
|
|
All’s Well that Ends Well
|
0
|
0
|
0
|
0
|
1.000
|
|
Othello
|
0
|
0
|
0
|
0
|
1.000
|
|
King Lear
|
0
|
0
|
0
|
0
|
1.000
|
|
Macbeth
|
0
|
0
|
1
|
1
|
0.681
|
|
Antony & Cleopatra
|
0
|
0
|
0
|
0
|
1.000
|
|
Pericles (Acts 3-5)
|
0
|
2
|
1
|
3
|
0.108
|
|
Coriolanus
|
0
|
1
|
0
|
1
|
0.681
|
|
Cymbeline
|
0
|
0
|
1
|
1
|
0.681
|
|
Tempest
|
0
|
1
|
0
|
1
|
0.681
|
|
Winter’s Tale
|
0
|
0
|
0
|
0
|
1.000
|
|
Two Noble Kinsmen (Sh)
|
0
|
1
|
2
|
3
|
0.108
|
|
Rd 1 tests: BoBs (1, 5, 7), semantic buckets, feminine endings, open
lines, slope tests, new words, rare words, no+not; Rd 2: contractions,
metrical fillers, I do; Rd 3: suffixes, prefixes, whereas/whenas,
adversions, most + modifiers.
* Poisson figures represent the expected proportion of plays having
the listed number of rejections or greater, based on the initial
35-play baseline. These proportions are revised in table 3, below,
after several plays are removed from that list.
|
-
The results suggest that, of the baseline plays,
3
Henry VI and
Titus Andronicus are collectively outside the range
of rejections we would expect to find for 35 Shakespearean plays. For instance,
we would expect to find texts with as many rejections as
3 Henry VI
(that is, five) at a rate of about 1 in every 200 plays, and texts with
as many rejections as
Titus Andronicus in only 2.4% of plays by Shakespeare
– or about 1 in 40.
[54] In addition to those two works,
a trio of other plays (
Hamlet, the Shakespeare-ascribed portion of
Two Noble Kinsmen, and the Shakespeare-ascribed portion of
Pericles)
have garnered three rejections each, though each individually should only
be 8% likely to have that many. Using a Bernoulli distribution, which calculates
the odds of multiple unlikely events (like 7 out of 10 coin flips landing
heads), we find that the probability five Shakespeare plays in a sample
of 35 would accumulate three or more rejections is 0.1554 – roughly a 15%
chance. Put another way, we would be almost 85% likely to be wrong if we
assumed Shakespeare wrote all five of the aforementioned plays solo.
-
So what can be made of these results? Do they mean Shakespeare
did not write
Hamlet? Not quite; such a conclusion would be rash
indeed. Yet they give us reason to believe that perhaps he did not write
all five of those works by himself. Scholars have already made convincing
arguments that some of these works were probably coauthored.
Titus Andronicus,
in particular, is now generally accepted as a collaboration,
[55] and such speculations are also old news for
3 Henry VI.
[56] The portions of
Pericles and
Two
Noble Kinsmen commonly assigned to Shakespeare may, in turn, be earning
rejections because the collaborative process affected all parts of the work
to some degree. Evidence gathered by Hope, for instance, is consistent with
the hypothesis that George Wilkins not only wrote the first two acts of
Pericles, but “was responsible for the reconstruction of the text”
from memory.
[57] Another explanation for the
results for
Pericles and
Two Noble Kinsmen might be that the
sample sizes were too small – once the clinic trimmed out the suspect portions
of the text – and thus produced more variance when tabulated.
[58] If one sets aside the plays that have likely
been affected by the hands of other authors or by surgery (
Titus Andronicus,
3 Henry VI, Pericles, and
Two Noble Kinsmen), then one is left
with only one apparent anomaly:
Hamlet. However, since we would expect
one or two plays out of 35 by Shakespeare to end up with precisely three
rejections, just by chance, we have little reason to be suspicious of the
Prince of Denmark. Once the other texts are set aside,
Hamlet looks
perfectly within bounds.
-
It is encouraging that none of the above results is particularly
surprising. The conclusions described above are not substantially different
from those initially reported by the clinic. The Claremont clinic, in its
debates with Foster, claimed that its tests were robust enough that they
could handle some erosion without changing the results significantly,
[59] and at least as far as the core plays are concerned,
this claim appears to be well-founded. Only the numbers of rejections, not
their relative proportions, have changed. In the meantime, the results help
demonstrate whether the Poisson distribution is a good tool for predicting
how often plays should generate given numbers of rejections. For Shakespeare,
the Poisson curves seem remarkably accurate. Once we eliminate the plays
that we already had good reason to believe are collaborations (
3H6, Titus)
and those which are partial and possibly tainted by other hands (
Pericles
and
Two Noble Kinsmen), we find that the rejection patterns of
the reduced sample match almost perfectly with what the reduced sample’s
new Poisson curve would predict, as evidenced by table 3.
|
Table 3: Poisson-based predictions for a reduced sample of 31
plays
|
|
No. of rejections
|
Expected no. of plays with # of rejections
|
Actual no. of plays with # of rejections
|
Revised Poisson for # of rejections or higher
|
|
0
|
13.83
|
13
|
1.000
|
|
1
|
11.16
|
11
|
0.554
|
|
2
|
4.5
|
5
|
0.194
|
|
3
|
1.2
|
1
|
0.048
|
|
4
|
0.244
|
0
|
0.009
|
|
5
|
0.039
|
0
|
0.002
|
-
This means we now have some idea of how many rejections
a play by Shakespeare should garner, but by itself this information does
not help us evaluate the writing of others. What are the odds that a play
by someone other than Shakespeare would get as few rejections as Shakespeare
does? We can hazard a guess by running Poisson distributions on the mean
number of rejections for plays believed to be by other authors. Claremont
has conveniently provided a large stable of 51 such plays, but the sweeping
date range for that large group (1567-1633) is problematic if we want the
sample to represent Shakespeare’s contemporaries. Rather than use that large
group (average rejections per play: 16.2) for my comparisons, I have trimmed
it down to just 24 plays with suspected composition dates between 1591 and
1611 (average rejections per play: 15.58). By doing so, we lose the advantage
of large sample size, but the lower, more contemporary average is closer
to Shakespeare’s own profile, and thus the more conservative approach.
-
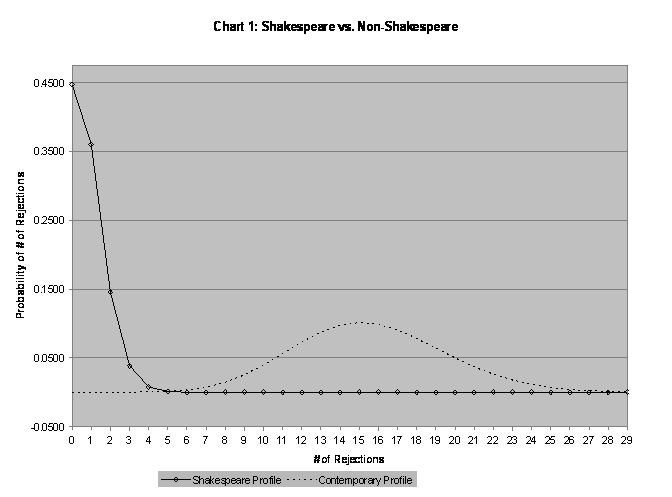
Chart 1 compares the Shakespeare curve for the reduced
sample to the contemporary proportion curve, revealing that plays with between
four and seven rejections should be fairly rare for both groups, and hard
to attribute easily. By enabling us to quickly compare two possible scenarios,
the chart enables us to better evaluate suspect works. A play with fewer
than four rejections is almost certainly by Shakespeare, at least in part.
A play with more than seven rejections has little hope of a solo Shakespeare
claim, though this does not preclude a collaborative role. A play with five
to six rejections, as we shall see below, is tougher to interpret. It is
an anomaly for both groups. While such a work might be a fluke, representing
a pattern of aberrant behavior by its author, it might well represent a
collaboration between Shakespeare and some other author.
-
Before proceeding, I must make some disclaimers about
the above curves. They assume that the Poisson distribution is as appropriate
for non-Shakespearean authors as it appears to be for Shakespearean plays.
Unfortunately, this is hard to evaluate by comparing frequency counts to
distribution models. The frequency distributions for the non-Shakesperean
groups (both the large one and the smaller, contemporary one) are trimodal
at best. That is, they do not form a bell curve, but generate three spikes
when graphed. Since most phenomena naturally fall into smooth curves, such
spikes are often evidence that other variables are interferring with the
results. I can think of two likely explanations for the trimodal spikes:
(1) Shakespearean collaborations might trigger a low-end spike; (2) chronological
factors might result in a late-play, high-end spike. The first possibility
must remain speculation, although we have strong qualitative, historical
reasons to believe that such collaboration happened often. The second, however,
can be verified, and appears consistent with the data. For plays believed
to be by authors other than Shakespeare, there appears to be a moderate
but significant, positive correlation (r=0.413, p=.003) between year of
composition and the number of rejections that the play receives. This correlation
only manifests for Shakespeare’s peers, not for Shakespeare himself. In
short, this trend means that late authors are even more unlike Shakespeare
than early authors are. Taken together, these phenomena help to explain
why the distribution of rejection totals for Shakespeare’s contemporaries
might be trimodal. Moreover, anything we might do to eliminate the low and
high spikes and produce a hypothetical, unimodal distribution based on standard
deviations runs into other problems. A normal distribution would for instance
be based on a high (and distorted) variance (s = 4.6), and thus seems unusable.
A negative binomial distribution, which might otherwise seem perfect, cannot
be used because the rejection rates for the tests are far from constant,
ranging from 16% to more than 60% (and if we average these rates to run
a negative binomial distribution, we end up with a curve that predicts nearly
a third of plays should have more than 27 rejections, when in fact none
do). For these reasons, I have gone again with the more restrictive Poisson
distribution, which does not depend on standard deviation, and which, judging
from the Shakespeare results and non-Shakespearean range, might be appropriate
anyway. Moreover, I assume that the two interferring variables just identified
roughly balance each other out, so that the overall average number of rejections
generated by the Contemporary Cluster is nevertheless representative of
the non-Shakespearean population.
-
Armed with the above chart and assumptions, we are now
ready to look at plays outside the canon and evaluate whether Shakespeare
might have had a part in writing them. Table 4 summarizes findings for selected
dubitanda and apocrypha. For each play, two cumulative Poisson-derived probabilities
are given: one assumes the play is by Shakespeare, the second that it is
not. With the two figures, one can compare the likelihoods of each scenario.
Table 4: Dubitanda and apocrypha
|
|
Play
|
Rd 1
|
Rd 2
|
Rd 3
|
Total
|
Non-Shakespeare Probability*
|
Shakespeare Probability **
|
|
Dubitanda
|
|
1 Henry VI
|
4
|
1
|
4
|
9
|
0.05303
|
0
|
|
Henry VIII (Fl)
|
4
|
5
|
4
|
13
|
0.30972
|
0
|
|
Henry VIII (Jt)
|
5
|
6
|
5
|
16
|
0.60723
|
0
|
|
Henry VIII (Sh)
|
2
|
5
|
4
|
11
|
0.14904
|
0
|
|
Pericles 1-2
|
3
|
5
|
5
|
13
|
0.30972
|
0
|
|
Timon of Athens
|
4
|
7
|
3
|
14
|
0.40725
|
0
|
|
TNK (Fl)
|
3
|
5
|
8
|
16
|
0.60723
|
0
|
|
TNK (Sh)
|
0
|
1
|
2
|
3
|
0.00013
|
0.048355
|
|
Titus Andronicus
|
2
|
0
|
2
|
4
|
0.00055
|
0.009329
|
|
Titus Andronicus (early stratum)
|
3
|
1
|
7
|
11
|
0.14904
|
0
|
|
Titus Andronicus (late stratum)
|
1
|
0
|
5
|
6
|
0.00525
|
0.000192
|
|
Sir Thomas More (Sh’s part)
|
3
|
5
|
9
|
17
|
0.69768
|
0
|
|
Apocrypha
|
|
Horestes
|
2
|
4
|
6
|
12
|
0.22212
|
0
|
|
Famous Victories of Henry V
|
3
|
5
|
5
|
13
|
0.30972
|
0
|
|
Taming of a Shrew
|
1
|
4
|
7
|
12
|
0.22212
|
0
|
|
Ironside
|
3
|
0
|
7
|
10
|
0.09276
|
0
|
|
Arden of Faversham
|
0
|
3
|
5
|
8
|
0.02754
|
0.000002
|
|
Contention of York, Part 1
|
0
|
2
|
8
|
10
|
0.09276
|
0
|
|
Contention of York, Part 2
|
3
|
1
|
6
|
10
|
0.09276
|
0
|
|
Guy of Warwick
|
3
|
6
|
5
|
14
|
0.40725
|
0
|
|
King Leir
|
2
|
2
|
3
|
7
|
0.01281
|
0.000022
|
|
Richard III
|
4
|
3
|
4
|
11
|
0.14904
|
0
|
|
Sir Thomas More
|
0
|
5
|
2
|
7
|
0.01281
|
0.000022
|
|
Edward III
|
5
|
2
|
5
|
12
|
0.22212
|
0
|
|
King John, Part 1
|
1
|
2
|
7
|
10
|
0.09276
|
0
|
|
King John, Part 2
|
2
|
3
|
6
|
11
|
0.14904
|
0
|
|
Locrine
|
8
|
6
|
3
|
17
|
0.69768
|
0
|
|
Woodstock
|
5
|
10
|
4
|
19
|
0.84021
|
0
|
|
Mucedorus
|
2
|
4
|
2
|
8
|
0.02754
|
0.000002
|
|
Sir John Oldcastle
|
1
|
5
|
5
|
11
|
0.14904
|
0
|
|
Thomas, Lord Cromwell
|
1
|
4
|
6
|
11
|
0.14904
|
0
|
|
The Merry Devil of Edmonton
|
2
|
7
|
1
|
10
|
0.09276
|
0
|
|
The London Prodigal
|
3
|
8
|
6
|
17
|
0.69768
|
0
|
|
The Puritan
|
3
|
12
|
5
|
20
|
0.89025
|
0
|
|
A Yorkshire Tragedy
|
3
|
8
|
4
|
15
|
0.50856
|
0
|
|
The Second Maiden’s Tragedy
|
5
|
17
|
3
|
25
|
0.99029
|
0
|
|
Double Falsehood
|
3
|
9
|
2
|
14
|
0.40725
|
0
|
|
Faire Em
|
2
|
8
|
8
|
18
|
0.77598
|
0
|
|
The Birth of Merlin
|
2
|
3
|
4
|
9
|
0.05303
|
0
|
|
The Revenger’s Tragedy***
|
2
|
17
|
5
|
24
|
0.98308
|
0
|
|
* Figures represent the proportion of plays by non-Shakespearean
authors that would be expected to earn the listed number of rejections
or lower.
** Proportions lower than 0.000002 are recorded here simply as 0.
Again, figures represent the proportion of plays that should have
the stated number of rejections or higher, based on the reduced Shakespeare
sample discussed earlier.
*** The Revenger’s Tragedy is included by Elliott and Valenza
because it is anonymous, not due to any Shakespearean attributions.
|
-
The figures in table 4 testify that the doubted plays
appear to have been doubted for good reason. Even relatively strong cases
like 1 Henry VI, Timon of Athens, and Edward III
receive, at best, limited support from the Claremont figures. Plays like
Arden of Faversham and King Leir do better, though certainly
not in the range of Shakespeare’s core plays, or even in the ballpark
of 3H6. It is tougher to interpret the results for the Shakespeare-ascribed
portions of Sir Thomas More and Henry VIII. At first glance,
it would appear both texts have been rejected. However, if we look to
the full text of Sir Thomas More, not just Shakespeare’s allotted
portion of it, we see that the overall play lands in the nebulous four-to-seven
range defined earlier – the sum of the text performs better than its part.
The best explanation for this strange disparity is, as noted earlier,
the fact that variance is often more extreme in small texts than in large
ones. Indeed, we see this same inconsistency surface in the only other
play for which we have both partial and complete data: Titus Andronicus.
The parts of Titus usually ascribed to Shakespeare fare worse
than the whole play does (six rejections, as opposed to four). I would
not be surprised if this same pattern repeats with plays like Henry
VIII, Pericles, or Two Noble Kinsmen (though
it is impossible to tell from the data set as currently reported, since
only partial results are provided for those plays). Assuming this is what
happened with Sir Thomas More, it is probably wisest to consider
the result for the whole play, which does indeed suggest the possibility
of collaboration.
-
There are additional, statistical reasons to consider
a collaborative interpretation in the above cases. It turns out that there
is a moderate but significant correlation (r=.365, p<.01) between a play’s
performance on the Claremont tests and whether it appears on table 4 or
table 5 (below), even after Two Noble Kinsmen and Titus Andronicus
and all of their associated strata are removed from the table 4 sample.
Since table 4 deals with suspected Shakespearean plays, and table 5 deals
with plays we suspect he did not write, the correlation implies that a significant
number of our suspicions about Shakespearean composition are correct. Indeed,
the probability that 11 out of any 35 non-Shakespearean plays would end
up with even as few as 10 rejections on Shakespeare-tempered tests (not
to mention 7 or 8) simply by chance is quite remote (0.00018), but this
is precisely what has happened with the plays in table 4. The smart way
to bet is that Shakespeare did not write those works solo, but that he was
a collaborator on several of them. Of the contenders for possible collaboration,
Sir Thomas More stands out, both as one of the better qualitative
cases, and as one of the better statistical ones.
-
What of the non-apocryphal plays, ones we believe to be
by other playwrights of the day? With few exceptions, the 51 plays in table
5 below look non-Shakespearean. Four plays, however, dip below the 10-rejection
barrier. The 1616 B text of The Tragical History of Doctor Faustus
and The Massacre of Paris both do as well as 1 Henry VI, with
nine rejections. Robert Wilson’s Three Ladies of London (written
a bit before Shakespeare’s day, in the early 1580s) fares still better,
with eight rejections. Matters of timing lead one to conclude Wilson’s result
is simply a matter of chance, and the probability that two plays out of
50 would do as well as Faustus and Massacre is roughly 0.25
– low, but not unreasonable. Thus, these three plays do well, but not to
a particularly noteworthy degree. However, the fourth of the strong performers
does surprisingly well and deserves elaboration.
|
Table 5: Presumed Non-Shakespearean Plays
|
|
Author
|
Play
|
Rd 1
|
Rd 2
|
Rd 3
|
Total
|
Non-Shakespeare Probability*
|
Shakespeare Probability**
|
|
Beaumont, Francis and Fletcher, John
|
The Knight of the Burning Pestle
|
3
|
10
|
3
|
16
|
0.607230724
|
0
|
|
Chapman, George
|
The Gentleman Usher
|
2
|
8
|
3
|
13
|
0.309732493
|
0
|
|
Chapman, George
|
Bussy D’Ambois
|
2
|
11
|
2
|
15
|
0.508559592
|
0
|
|
Daniel, Samuel
|
Cleopatra
|
2
|
4
|
7
|
13
|
0.309732493
|
0
|
|
Dekker, Thomas
|
The Whore of Babylon
|
5
|
10
|
5
|
20
|
0.890247765
|
0
|
|
Dekker, Thomas
|
Honest Whore
|
7
|
7
|
7
|
21
|
0.927381014
|
0
|
|
Fletcher, John
|
The Woman’s Prize
|
3
|
10
|
1
|
14
|
0.407249978
|
0
|
|
Fletcher, John
|
Valentinian
|
0
|
8
|
6
|
14
|
0.407249978
|
0
|
|
Fletcher, John
|
Monsieur Thomas
|
5
|
5
|
2
|
12
|
0.222123015
|
0
|
|
Fletcher, John
|
Chances
|
3
|
10
|
4
|
17
|
0.697679068
|
0
|
|
Fletcher, John
|
The Loyal Subject
|
4
|
11
|
4
|
19
|
0.84020713
|
0
|
|
Fletcher, John
|
Demetrius and Enanthe
|
3
|
6
|
3
|
12
|
0.222123015
|
0
|
|
Fletcher, John
|
Sir J.V.O. Barnavelt
|
1
|
8
|
3
|
12
|
0.222123015
|
0
|
|
Fletcher, John
|
The Island Princess
|
3
|
10
|
4
|
17
|
0.697679068
|
0
|
|
Greene, Robert
|
Alphonsus
|
4
|
4
|
5
|
13
|
0.309732493
|
0
|
|
Greene, Robert
|
Friar Bacon & Friar Bungay
|
6
|
3
|
7
|
16
|
0.607230724
|
0
|
|
Greene, Robert
|
James IV
|
2
|
5
|
7
|
14
|
0.407249978
|
0
|
|
Heywood, Thomas
|
A Woman Killed with Kindness
|
1
|
9
|
2
|
12
|
0.222123015
|
0
|
|
Jonson, Ben
|
Sejanus
|
3
|
5
|
3
|
11
|
0.149036877
|
0
|
|
Jonson, Ben
|
Volpone
|
2
|
9
|
3
|
14
|
0.407249978
|
0
|
|
Jonson, Ben
|
The Alchemist
|
5
|
10
|
6
|
21
|
0.927381014
|
0
|
|
Jonson, Ben
|
Bartholomew Fair
|
5
|
9
|
4
|
18
|
0.775983717
|
0
|
|
Jonson, Ben
|
The New Inn
|
4
|
6
|
5
|
15
|
0.508559592
|
0
|
|
Jonson, Ben
|
A Tale of a Tub
|
4
|
10
|
9
|
23
|
0.971504644
|
0
|
|
Kyd, Thomas
|
The Spanish Tragedy
|
4
|
3
|
7
|
14
|
0.407249978
|
0
|
|
Lyly, John
|
The Woman in the Moon
|
7
|
8
|
5
|
20
|
0.890247765
|
0
|
|
Marlowe, Christopher
|
Tamburlaine
|
8
|
5
|
9
|
22
|
0.953683676
|
0
|
|
Marlowe, Christopher
|
Tamburlaine, pt. 2
|
7
|
5
|
6
|
18
|
0.775983717
|
0
|
|
Marlowe, Christopher
|
Doctor Faustus, 1616
|
1
|
2
|
6
|
9
|
0.053029128
|
0
|
|
Marlowe, Christopher
|
The Jew of Malta
|
1
|
5
|
6
|
12
|
0.222123015
|
0
|
|
Marlowe, Christopher
|
Edward II
|
0
|
3
|
3
|
6
|
0.005253317
|
0.000192
|
|
Marlowe, Christopher
|
The Massacre at Paris
|
1
|
1
|
7
|
9
|
0.053029128
|
0
|
|
Marlowe, Christopher
|
Dido, Queen of Carthage
|
7
|
2
|
6
|
15
|
0.508559592
|
0
|
|
Middleton, Thomas
|
The Phoenix
|
2
|
12
|
3
|
17
|
0.697679068
|
0
|
|
Middleton, Thomas
|
Michaelmas Term
|
5
|
14
|
4
|
23
|
0.971504644
|
0
|
|
Middleton, Thomas
|
A Chaste Maid Cheapside
|
6
|
15
|
4
|
25
|
0.99028859
|
0
|
|
Middleton, Thomas
|
No Wit Like a Woman’s
|
5
|
16
|
2
|
23
|
0.971504644
|
0
|
|
Middleton, Thomas
|
More Dissemblers
|
7
|
15
|
4
|
26
|
0.994611588
|
0
|
|
Middleton, Thomas
|
The Witch
|
4
|
14
|
6
|
24
|
0.983075873
|
0
|
|
Middleton, Thomas
|
Hengist/Mayor of Queenboro
|
3
|
11
|
3
|
17
|
0.697679068
|
0
|
|
Middleton, Thomas
|
Women Beware Women
|
5
|
14
|
3
|
22
|
0.953683676
|
0
|
|
Middleton, Thomas
|
A Game at Chess
|
5
|
12
|
6
|
23
|
0.971504644
|
0
|
|
Munday, Anthony
|
John a Kent and John a Cumber
|
3
|
3
|
5
|
11
|
0.149036877
|
0
|
|
Nashe, Thomas
|
Will Summer’s Last Will & Testa.
|
8
|
3
|
2
|
13
|
0.309732493
|
0
|
|
Peele, George
|
The Arraignment of Paris
|
7
|
4
|
6
|
17
|
0.697679068
|
0
|
|
Peele, George
|
David and Bethsabe
|
6
|
7
|
6
|
19
|
0.84020713
|
0
|
|
Pickering, John
|
Horestes
|
2
|
4
|
6
|
12
|
0.222123015
|
0
|
|
Porter, Henry
|
Two Angry Women of Abingdon
|
3
|
5
|
9
|
17
|
0.697679068
|
0
|
|
Sidney Herbert, Mary
|
Antonius (extract)
|
9
|
5
|
7
|
21
|
0.927381014
|
0
|
|
Smith, Wm. (Wentworth)
|
The Hector of Germany
|
3
|
5
|
3
|
11
|
0.149036877
|
0
|
|
Wilson, Robert
|
Three Ladies of London
|
2
|
3
|
3
|
8
|
0.027535558
|
0.000002
|
|
* Figures represent the proportion of plays by non-Shakespearean
authors that would be expected to earn the listed number of rejections
or lower.
|
|
** Proportions lower than 0.000002 are recorded here simply as 0.
Again, figures represent the proportion of plays that should have
the stated number of rejections or higher, based on the reduced Shakespeare
sample discussed earlier.
|
The curious matter of Edward II
-
When we remove the suspect Morton-regime tests and BoB3,
we find that Edward II has become a statistical outlier for both
Shakespeare and for his contemporaries. The play, normally attributed to
Marlowe, has just six rejections – as many as the Shakespeare-ascribed portion
of Titus Andronicus, fewer than any of the other dubitanda or apocryhpa
including 1 Henry VI and Timon of Athens, and two fewer rejections
than the next-closest work on table 5. Even before the revised rejection
counts, Edward II looked peculiar, with just 10 rejections, compared
with a Marlovian average of 16. In fact, no matter how one slices the results,
Edward II fares much better here than does Edward III (12
rejections in my revised count), even though the latter play is increasingly
being accepted as Shakespearean, to the point of inclusion in the second
edition of the Riverside Shakespeare and the Oxford Complete Works.
Such a result begs for an explanation.
-
Claremont’s is not the first study to uncover something
unusual about the play, incidentally. In
William Shakespeare: A Textual
Companion, Taylor runs a function word test developed by Marvin Spevack
[60]
on plays by Marlowe and Shakespeare, and concludes the two were clearly
different authors. On the basis of their tests, he easily dismisses the
purely hypothetical possibility that Shakespeare might have written works
such as
Tamburlaine the Great, Part I. Yet he notes in passing that
he cannot similarly falsify Shakespearean authorship of
Dido, Queen of
Carthage;
Edward II; or
The Jew of Malta, because they
do not garner enough rejections for out-of-hand dismissal.
[61]
What he writes next seems particularly interesting in light of the modified
Claremont results: He concludes that
Edward II is the most Shakespearean
of the non-canon works tested, even more Shakespearean than frequently discussed
apocrypha like
Arden of Faversham and
Edward III. Nevertheless,
rather than focusing on why
Edward II fared so well, he speculates
that
Edward III might have fared poorly due to collaboration.
[62] Indeed, Taylor hastens to clarify his position
on
Edward II, lest readers draw the wrong conclusion:
In making such observations I do not mean to raise seriously
the possibility that Shakespeare wrote Edward II; I am merely discriminating
between two uses of the function word test. [… Y]ou can confidently say
that the [Marlowe] group is statistically incompatible with the Shakespeare
group. On the other hand, if you consider some of the works in the Marlowe
group individually, you could not prove, on the basis of this test alone,
that Shakespeare did not write them.[63]
Edward II is, in fact, so far from consideration by Taylor that it
does not even warrant a listing on his list of “works excluded,” though
less-Shakespearean apocrypha like
Edmund Ironside,
The Birth of
Merlin, and
Edward III do appear there.
[64]
-
It is important to keep in mind that the function word
test used by Taylor is an entirely different and independent metric from
those employed by the Claremont team, and thus might be expected to produce
different results. That the test seems to corroborate the Claremont battery
is, then, all the more intriguing. While it is certainly possible that both
of the independent results are somehow flukes or errors, the correspondence
suggests this is unlikely.
[65] More probable explanations exist, and prudence
dictates that we weigh and analyze them before dismissing the results as
spurious or flawed.
-
One possibility is that we are seeing signs of imitation.
This would hardly, in fact, be a new hypothesis for
Edward II. To
cite but one example, David V. Erdman and Ephim G. Fogel, in their comprehensive
annotated bibliography to
Evidence for Authorship: Essays on Problems
of Attribution, discuss evidence that Marlowe and Shakespeare might
have been associates in Pembroke’s company at the dawn of Shakespeare’s
career, and note (like many other readers) that
Edward II varies
structurally from Marlowe’s other plays while bearing similarities to the
Henry VI plays. Marlowe, they speculate, might have been imitating
that early Shakespearean tetralogy.
[66] Other variations on the imitation
hypothesis are possible, of course: Shakespeare might have been imitating
Edward II. That is, if Shakespeare had fixated early in his career
on Marlowe’s
Edward II as a model for emulation, and if he had gained
enough exposure to it (perhaps as an actor), signs of that fixation might
appear throughout the canon, triggering a low rejection count for his model.
-
However, imitation good enough to replicate adversion
frequencies per 20,000 words (along with nearly 40 other metrics) is a bit
tougher than attribution skeptics sometimes suppose. As tempting as imitation
hypotheses can be, we should keep in mind that common authorship sometimes
looks a lot like imitation if one of the initial attributions is wrong,
a point nicely demonstrated by Foster’s work on
A Funeral Elegy.
Assuming Shakespeare wrote
A Funeral Elegy, Foster concluded that
the poem influenced John Ford’s own verse. Yet it now appears that Foster
should have followed that line of thinking more diligently: Ford, it seems,
was not influenced by the
Elegy – it appears he wrote the
Elegy.
[67]
-
Despite these brief cautions, however, it remains possible
that authors who have worked closely together (as Erdman and Fogel suppose
may have happened with our two suspects) could develop styles similar enough
to partially throw off attributionists, through a process termed
accommodation.
[68] Of course, one of the better
springboards to accommodation is collaboration by the authors,
[69] an observation that invites us to consider
collaborative explanations for the
Edward II outlier.
-
Like the imitation hypothesis, the collaborative hypothesis
has two chief variants. One, the division scenario, holds that Marlowe and
Shakespeare wrote
Edward II together, in which case experience with
other jointly-authored plays tells us to look for a division of labor similar
to those found or suspected for plays like
Titus Andronicus,
Timon
of Athens,
Pericles, and
Henry VIII, and well established
for works like
Sir Thomas More, Machiavelli and the Devil, Isle of Dogs,
and
The Late Murder in Whitechapel, or Keep the Widow Waking.[70] Evidence surrounding the above titles suggests that divvying
up of acts and scenes was a natural and normal expedient in a fast-moving
theatrical marketplace,
[71]
so even for a play like
Edward II (which lacks clean act and scene
divisions) it might be fruitful to look for a division of labor.
-
A second variant is the revision scenario, which speculates
that one author wrote the play and then another author revised it, resulting
in the
Edward II text we have today. We know from the work of scholars
like Gerald Eades Bentley that companies often kept, reworked, and updated
successful plays, rewriting parts to reflect changes in available cast members,
to market a play as containing new songs, and to take advantage of hot topics
or avoid taboos.
[72] In an interesting complement
to this point, C.F. Tucker Brooke hypothesizes – based on secondary evidence
– that a 1593 edition of
Edward II (long since lost) might have been
rushed to press hastily after Marlowe’s death bearing transcriptional errors
later eliminated in surviving editions,
[73] and if this is true, the version we have today represents a
revision by someone. Of course, even the 1594 version's missing stage directions,
variable speech prefixes, and absence of act and scene divisions look to
some editors like “authorial casualness,”
[74]
so it is not entirely clear who revised the text or how substantial that
revision was. Nevertheless, it would not be at all unusual for a play like
Edward II to be revised by another playwright while it is still in
the company repertoire, and Shakespeare’s hand in
Sir Thomas More
suggests casualness on his part, too.
- Without endorsing the above scenario specifically, my own instinct is that
revision is somewhat more plausible than division is, in part because Edward
II lacks the severe breaks in style or continuity so common to piecemeal
composition. (As Vickers remarks, “Unity is a rare commodity in co-authored
plays.”[75] If Edward II
is indeed an assembled play, it is a rare gem among its kind.) Moreover, even
if we count Love’s Labour’s Lost, few Shakespeare plays are as permeated
by Latin as is Edward II, a feature that – along with the prosody,
which seems Marlovian at its core – suggests Marlowe’s hand throughout, rather
than in parts.
- Of course, any collaborative argument has hurdles to overcome. A major
obstacle in this case is the near-total absence of external evidence in its
favor. Edward III at least has the virtue of being anonymous, inviting
attribution. Edward II, on the other hand, is clearly ascribed to a
single author: Marlowe. Indeed, the only commonly referenced external evidence
for a Shakespearean hand in Edward II – a 1656 publisher’s catalog
that assigns the play, along with Edward III and Edward IV to
him[76] – is quite reasonably
taken with a grain of salt by scholars. Although we have come to accept that
having Shakespeare’s name on a cover does not necessarily mean he was without
a helping hand, external evidence still counts for something, and it would
be reckless to cast it aside without more compelling internal evidence.
- Coming up with such internal evidence for the revision scenario might be
rather thorny, of course, as the methodologies for identifying revision seem
more uncertain than those for breaking out divisions, and, being more statistically
complicated, are tougher to sell to mixed audiences. One of the few attributionists
to examine plays closely for evidence of Shakespearean revision is Thomas
Merriam. In one 1996 study, he suggests that context-specific word choice
similarities between Marlowe’s work and Shakespeare’s history plays are better
explained by “Shakespeare’s incorporation and revision of original writing
by Marlowe” than by influence or imitation,[77] a thesis he explores in several articles positing
Shakespearean revisions of Marlovian works.[78] However, Merriam’s strange ascription
of 90% of Sir Thomas More to Shakespeare, along with M.W.A. Smith’s
elaborate discrediting of his methods in the 1980s, have earned Merriam his
share of skeptics.[79] And,
unfortunately, few other researchers have immersed themselves in such work,
leaving us at the moment with little to go on but suspicion where the revision
scenario is concerned.
- Regardless of the challenges facing any given explanation, however, the
Edward II results represent a clear anomaly. The play’s authorship
deserves more attention. A reasonable course of action at this point would
be to single out the most likely scenarios and attempt to falsify them. The
explanation that best withstands rigorous scrutiny is probably the correct
one. Perhaps additional tests will eliminate the play from Shakespearean consideration
more conclusively, or maybe Edward II is simply a statistical outlier
for Marlowe. Perhaps Marlowe was imitating his fellow playwright, or perhaps
Edward II was Shakespeare’s favorite play, and had a significant impact
on his later work. Nevertheless, with the Claremont results showing that Edward
II is an anomaly for both authors, too un-Shakespearean for Shakespeare
and too Shakespearean for Marlowe, scholars also might want to consider “seriously”
(as Wells and Taylor did not) the possibility of mixed authorship.
[1] Don Foster, “Response to Elliot [sic] and Valenza, ‘And Then There
Were None,’” Computers and the Humanities 30 (1996):, 250.
[6] Ward E. Y. Elliott and Robert J. Valenza, “The Professor Doth Protest
Too Much, Methinks: Problems with the Foster ‘Response,’” Computers and
the Humanities 32 (1999): 428.
[7] See Brian Vickers,
Shakespeare, Co-Author: A Historical Study of Five Collaborative Plays
(Oxford: Oxford University Press, 2002).
[8] Rick Abrams and Don Foster, “Abrams and Foster on ‘A Funeral Elegy,’”
SHAKSPER: The Global Electronic Conference, SHK 13.1514, online message
board moderated by Hardy M. Cook, June 13, 2002, http://www.shaksper.net/archives/2002/1484.html
(accessed May 14, 2005).
[9] Brian Vickers, Counterfeiting Shakespeare: Evidence, Authorship,
and John Ford’s Funerall Elegye (Cambridge: Cambridge University Press,
2002), 196.
[11] Joseph Rudman, “The State of Authorship Attribution Studies: Some
Problems and Solutions,” Computers and the Humanities 31 (1998):
351-365.
[12] David Joseph Kathman, “Don Foster and the Funeral Elegy,” transcript
of an online exchange at ShakespeareAuthor-ship.com, n.d., http://www.shakespeareauthorship.com/elegydf.html,
par. 5 (accessed May 14, 2005).
[13] Thomas Merriam, “Tamburlaine Stalks in Henry VI,” Computers
and the Humanities 30 (1996): 280.
[14] MacDonald P. Jackson, “Pause Patterns in Shakespeare’s Verse: Canon
and Chronology,” Literary and Linguistic Computing 17, no. 1 (2002):
39. See also Ants Oras, Pause Patterns in Elizabethan and Jacobean Drama:
An Experiment in Prosody (University of Florida Monographs, Humanities
No. 3, Winter 1960. Gainsville, Fla.: University of Florida Press, 1960).
[15] David Joseph Kathman, “Re: Funeral Elegy,” SHAKSPER: The Global Electronic
Conference, SHK 7.0116, message board moderated by Hardy M. Cook, Feb. 15,
1996, http://www.shaksper.net/archives/1996/0119.html (accessed May 14,
2005).
[16] Don Foster, “The Claremont Shakespeare Authorship Clinic: How Severe
Are the Problems?” Computers and the Humanities 32 (1999): 496.
[17] Ward E. Y. Elliot and Robert J. Valenza, “So Many Hardballs, So Few
Over the Plate: Conclusions from Our ‘Debate’ with Donald Foster” (unpublished,
expanded version of article that appeared in Computers and the Humanities
36 [see note #49], Claremont McKenna College, Oct. 26, 2002), http://govt.claremontmckenna.edu/welliott/hardball.htm,
sec. 3.2, pts. 13-14 (accessed May 14, 2005, emphasis added). Because Computers
and the Humanities did not give the authors as much space as they felt
they needed to respond properly to Foster’s attacks, they posted a lengthier
(and often more informative) version online.
[18] Vickers, Counterfeiting Shakespeare, 448.
[20] Elliott and Valenza, “So Many Hardballs” (unpublished version), sec.
2.4.
[21] Ward E. Y. Elliott and Robert J. Valenza, “And Then There Were None:
Winnowing the Shakespeare Claimants,” Computers and the Humanities
30 (1996): 196. An example: Suppose a typical play by John Doe has 9 occurrences
of the word “clever” (a Doe badge) and just 1 occurrence of “smart” (a Doe
fluke) per 20,000 words. [9-1]/[9+1] = 8/10 = 0.8. Now compare this with
another play in which the counts are 4 and 6: -2/10 = -0.2. Clearly the
first play fits the profile better than the second.
[22] Foster, “Response,” 251.
[23] I have excluded the Shakespeare canon plays from this correlation
test and those that follow because the presence of a single author behind
half of the sample would reasonably be expected to interfere with the results.
I have also picked p < .05 as my standard for two-tailed significance.
For this problem, I have set r < 0.7 and r > -0.7 as the range of
acceptable multicollinearity, considering figures higher than 0.7 or lower
than -0.7 to be problematic.
[24] It does not much matter
to the accepted Shakespeare canon whether we eliminate BoB1 or BoB3, since
these two tests reject in perfect tandem for plays attributed to Shakespeare.
Where they differ, sometimes, is in their reporting on plays believed to
be by other hands.
[25] Foster, “Response,” 252.
[26] Rudman, “State of Authorship Attribution,” 355.
[27] Elliott and Valenza, “The Professor Doth Protest Too Much,” 436 (emphasis
in original).
[28] The period in question was one of great linguistic flux and change,
so it might be unrealistic to expect no correlation at all, even in tests
that are otherwise reliable. To eliminate tests with moderate-to-high correlations
while allowing for the inevitable weakly correlated (but probably still
useful) test, I have set my range for acceptable correlation at r > -0.35
and r < 0.35.
[29] Rudman, “The State of Authorship Attribution,” 355. For a more authoritative
answer on the Thisted-Efron test specifically, including a discussion about
why the test might not be suitable for poems, see Robert J. Valenza, “Are
the Thisted-Efron Authorship Tests Valid?” Computers and the Humanities
25 (1991): 27-46.
[30] Sharon Kunoff and Sylvia Pines, “Teaching Elementary
Probability through Its History,” The College Mathematics Journal
17, no. 3 (May 1986): 210-219. See also F.N. David, Games, Gods, and
Gambling (New York: Hafner, 1962) for a more thorough discussion of
statistical history.
[31] E. Bruce Brooks, “Tales of Statisticians: Siméon Denis Poisson,” Acquiring
Statistics: Techniques and Concepts for Historians (University of Massachusetts,
2001), http://www.umass.edu/wsp/statistics/tales/poisson.html, par. 4 (accessed
May 14, 2005).
[32] Foster, “Claremont Shakespeare Authorship Clinic,” 498.
[33] Foster, “Response,” 250.
[34] Foster, “Claremont Shakespeare Authorship Clinic,” 495.
[35] Rudman, “State of Authorship Attribution,” 354.
[36] Ward E. Y. Elliott and Robert J. Valenza, “So Many Hardballs, So Few
Over the Plate: Conclusions from Our ‘Debate’ with Donald Foster,” Computers
and the Humanities 36 (2002): 457.
[37] Elliott and Valenza, “And Then There Were None,” 215.
[38] Vickers, Counterfeiting Shakespeare, 196.
[39] Foster may be speaking from experience here, if Elliott and Valenza’s
accusations are correct.
[40] Foster, “Response,” 249-250.
[41] Jonathan Hope, The Authorship of Shakespeare’s Plays: A Socio-Linguistic
Study (Cambridge: Cambridge University Press, 1994), 8.
[42] Stanley Wells, Gary Taylor, John Jowett, William Montgomery, William
Shakespeare: A Textual Companion (Oxford: Clarendon Press, 1987), 80.
[43] Andrew Queen Morton, Literary Detection: How to Prove Authorship
and Fraud in Literature and Documents (Bath, U.K.: The Pitman Press,
1978), 38.
[44] Vickers, Shakespeare Co-Author, 39-40.
[45] Hope, Authorship of Shakespeare’s Plays, 140.
[46] Elliott and Valenza, “And Then There Were None,” 195.
[47] Elliott and Valenza, “So Many Hardballs,” 457.
[48] Elliott and Valenza, “And Then There Were None,” 209.
[50] See Karl Popper, The Logic
of Scientific Discovery (New York: Harper Torchbooks/Harper & Row,
1968).
[51] Foster, “The Claremont Shakespeare Authorship Clinic,” 499-501.
[52] I noted earlier that Elliott and Valenza have conducted this experiment
in part (see “And Then There Were None,” 208-209). However, the results
of these edition-versus-edition tests of have not been published
in enough detail for bystanders to judge whether the variance among editions
would result in false rejections to Shakespeare plays for most of the tests
in doubt here. For instance, their reported ±20% variance around the mean
for the hyphenated compound word test does not look like it would affect
pass rates much, but the same spread might very well have an impact on rejection
counts for the grade-level tests; without complete information, it is hard
to tell. To truly judge the Morton tests, we need rejection rates for the
competing editions, in addition to variances. Also, the comparisons only
appear to have been made for grade level and hyphenated compound words,
not for the other tests in question.
[53] The approach of weighing plays written before 1608 by one standard
and later plays by another is laudable in that it accommodates changing
practices. One drawback critics should consider is that such an approach
relies on having accurate composition dates – if the accepted date is wrong,
the test result might be, too. For the purposes of this analysis, however,
I am accepting the dates and results as given, in part because both seem
consistent with scholarly consensus.
[54] Although we might expect two true plays in a random sample of 35 works
to register as false on any single test, simply by chance, the situation
here is more complicated than that: We’re looking at the results of a constellation
of 44 tests, not just one test. Each of those tests passes 95% or more of
the plays in the Shakespearean corpus. If a particular play generates many
rejections on these tests, I am inclined to agree with Elliott and Valenza
that “the glaring rejection clusters are ‘spikes,’ not flukes, and that
one would hardly expect to find so many together by chance” (see Elliott
and Valenza, “And Then There Were None,” 195).
[55] Vickers, Shakespeare Co-Author, chap. 3.
[56] Herschel Baker, “Henry VI, Parts 1, 2, and 3,” in The Riverside
Shakespeare: The Complete Works, 2nd ed, ed. G. Blakemore
Evans, J.J.M. Tobin, et al. (Boston: Houghton Mifflin Co., 1997), 623-629.
[57] Hope, Authorship of Shakespeare’s Plays, 113.
[58] Elliott and Valenza, “And Then There Were None,” 195.
[59] Elliott and Valenza, “The Professor Doth Protest Too Much,” 425.
[60] Wells and Taylor, William Shakespeare: A Textual Companion,
80-81.
[63] Ibid., 83 (emphasis added).
[64] Ibid., 134-141. On a similar note, Valenza’s aforementioned “Are
the Thisted-Efron Authorship Tests Valid?” observes that little consistency
appears when Thisted-Efron tests – which prove valid for authors like Shakespeare
– are run comparing Marlowe’s Tragical History of Doctor Faustus
to the rest of the Marlovian corpus (38). Given the small size of the corpus
in question, one can easily imagine that any collaboration (no matter which
play it appears in) would make it difficult to match Marlowe to Marlowe
on some tests.
[65] Indeed, flukes are unlikely by definition. It’s possible, as noted
earlier, that the Poisson distribution is not a perfect fit for non-baseline
plays, and thus might be misrepresenting the probabilities for non-Shakespearean
authorship somewhat. Even if the probabilities could be more finely tuned,
however, the play stands out simply for its rejection total, and the basic
observation that something appears to be off with Edward II remains.
[66] David V. Erdman and Ephim G. Fogel, ed., Evidence for Authorship:
Essays on Problems of Attribution, (Ithaca, New York: Cornell University
Press, 1966), 443.
[67] Abrams and Foster, “Abrams and Foster on ‘A Funeral Elegy.’”
[68] Hope, The Authorship of Shakespeare’s Plays, 79.
[69] Another avenue to accommodation might be acting. If Shakespeare frequently
performed Marlowe’s work, he might have internalized enough of his style
to imitate him well. However, to use this notion as an explanation for the
Edward II result, one would have to assume Shakespeare had focused
most of his attention on that play, or else one would expect the entire
Marlovian canon to do as well as Edward II.
[70] See chapter 8 of Gerald Eades Bentley. The Profession of the Dramatist
in Shakespeare’s Time, 1590-1642. (Princeton, New Jersey: Princeton
University Press, 1971). See also Vickers, Shakespeare Co-Author,
27-43.
[71] Vickers, Shakespeare
Co-Author, 27-29.
[72] Bentley, Profession of the Dramatist in Shakespeare’s Time, chapter
9.
[73] C. F. Tucker Brooke, “On the Date of the First Edition of Marlowe’s
Edward II,” Modern Language Notes 24, no. 3 (1909): 71-73.
[74] David Bevington and Eric Rasmussen, ed. Doctor Faustus and Other
Plays, by Christopher Marlowe. (Oxford: Oxford University Press, 1998),
xxix-xxx.
[75] Vickers, Shakespeare
Co-Author, 29.
[76] Hope, Authorship
of Shakespeare’s Plays, 134.
[77] Merriam, “Tamburlaine Stalks,” 280.
[78] See Thomas Merriam, “Edward III,” Literary and Linguistic
Computing 15 (2000): 157; Thomas Merriam, “King John Divided,”
Literary and Linguistic Computing 19.2 (2004): 181; and Thomas Merriam,
“Heterogeneous Authorship in Early Shakespeare and the Problem of Henry
V,” Literary and Linguistic Computing 13 (1998): 15.
[79] For a solid recounting
of the debates between Merriam and Smith, see Vickers, Shakespeare Co-Author,
110-111; 321-322.
Responses to this piece intended for the
Readers' Forum may be sent to the Editor at M.Steggle@shu.ac.uk. ©
2006-, Matthew Steggle (Editor, EMLS).
©
2006-, Matthew Steggle (Editor, EMLS).